Academic Collaboration
UGA - Myanmar Universities
in Applied Mathematics
|
|
Academic CollaborationUGA - Myanmar Universitiesin Applied Mathematics |
|
|
|
2021 : UGA-Myanmar Training in Applied-Maths
2021 : UGA-Myanmar : Kinect 3D-Project
2022 : UGA-Myanmar Training in Applied-Maths
This project concerns the development of a joint curriculum in applied mathematics between Université Grenoble-Alpes (UGA) and several academic institutions in Myanmar. Since a few years, Myanmar has opened up to international cooperation, particularly in science and education. Its universities have been modernized and are expected to play a greater role in the shaping of the nation's future. In strategic areas such as scientific computing, data analysis, numerical modelling, which require specific infrastructure and qualified instructors, they have not yet reached standard international training capacities.
Provide a series of theoretical and practical hands-on courses in applied mathematics and numerical computing
to undergraduate students of mathematics and computer science, of the same level as those offered at UGA.
Provide high-level specialized training for instructors in Myanmar, who will deliver the courses locally.
Encourage some Myanmar students in applied mathematics and computer science to enrol in UGA masters
programs.
This projects originates from visits of Luc Biard, Professor of Mathematics
at UGA, to Myanmar in 2016, 2017 and 2018.
During these visits, the French Institute of Burma (IFB) helped Prof. Biard
establish contacts with representative of several universities and educational
institutions in Myanmar.
The IFB develops cultural activities in Yangon and is in charge of promoting
the French culture throughout Myanmar.
In 2017, Prof. Biard gave a course in applied math at Dagon University
to demonstrate the relevance of software tools (like Scilab or Python)
and lab work in the teachings of modern computational mathematics.
This course was highly appreciated by the math teachers that attended it,
and in particular by Dr Aye Aye Tun, then pro-rector of Dagon University,
who invited Prof. Biard to think of a way to incorporate these courses
in the curriculum of Dagon University and invited him to visit again the
following year.
Following this visit, Ms. Zin Zar Aung, student at Dagon University,
was offered a IFB scholarship to study at UGA during the academic year 2017-18,
where she enrolled in the Mathematics-Computer Science (MIN)
bachelor program.
In 2018, Prof. Biard gave a course at Dagon University and visited UCSI, Bago
and Maubin universities.
Math teachers expressed their desire to increase their knowledge on
applied and computational mathematics.
Dr. Aye Aye Tun explicitely expressed her interest in finding ways
to sustain this type of cooperation between UGA and Myanmar Universities.
|
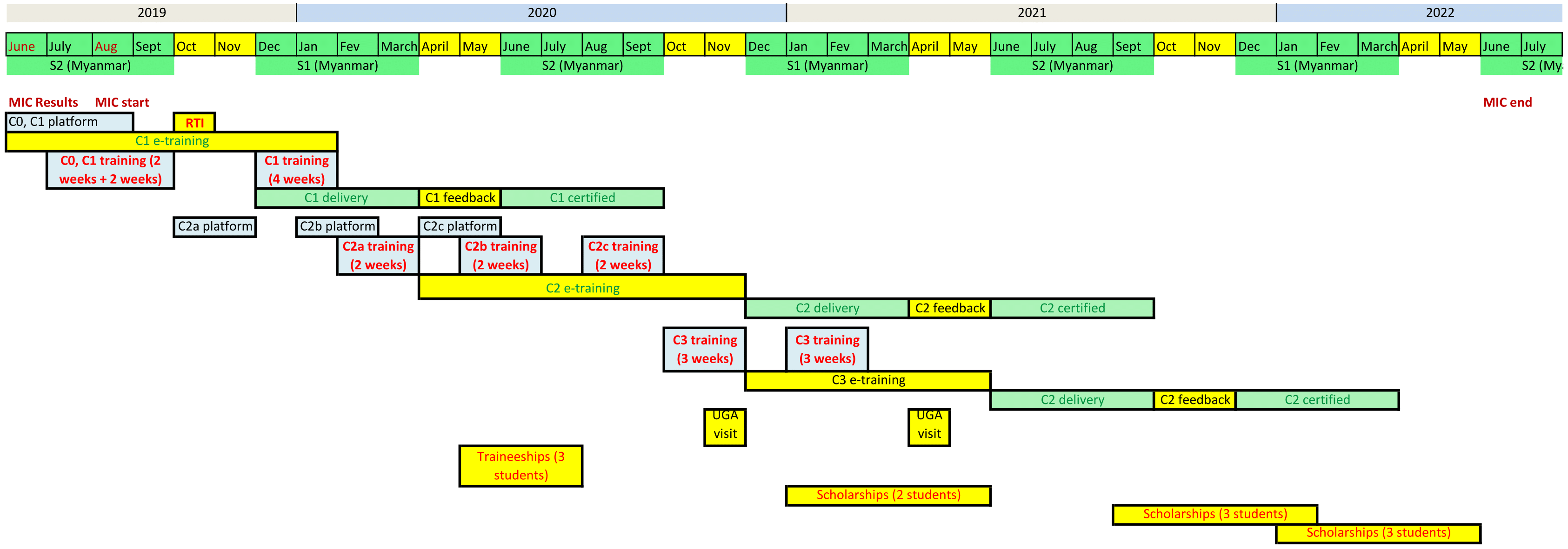
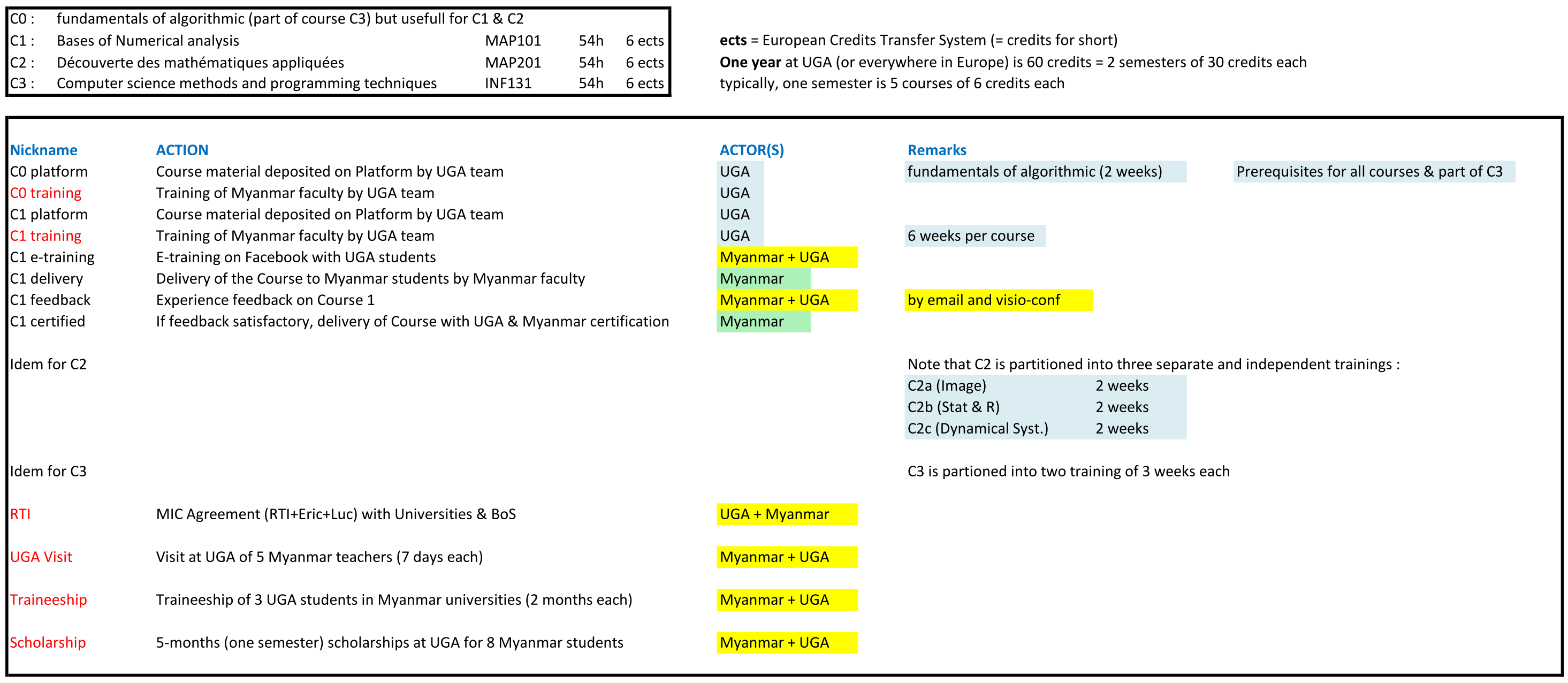
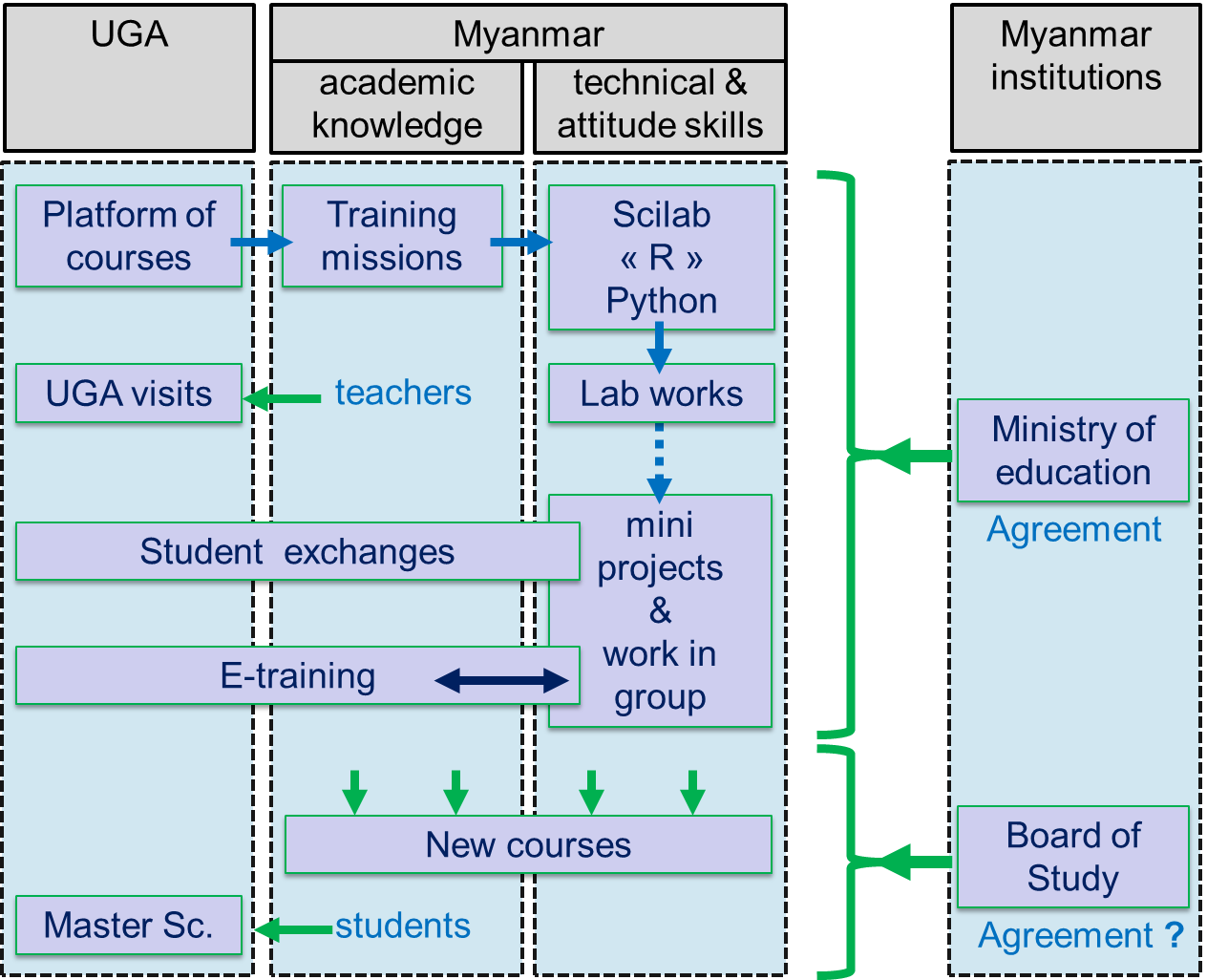
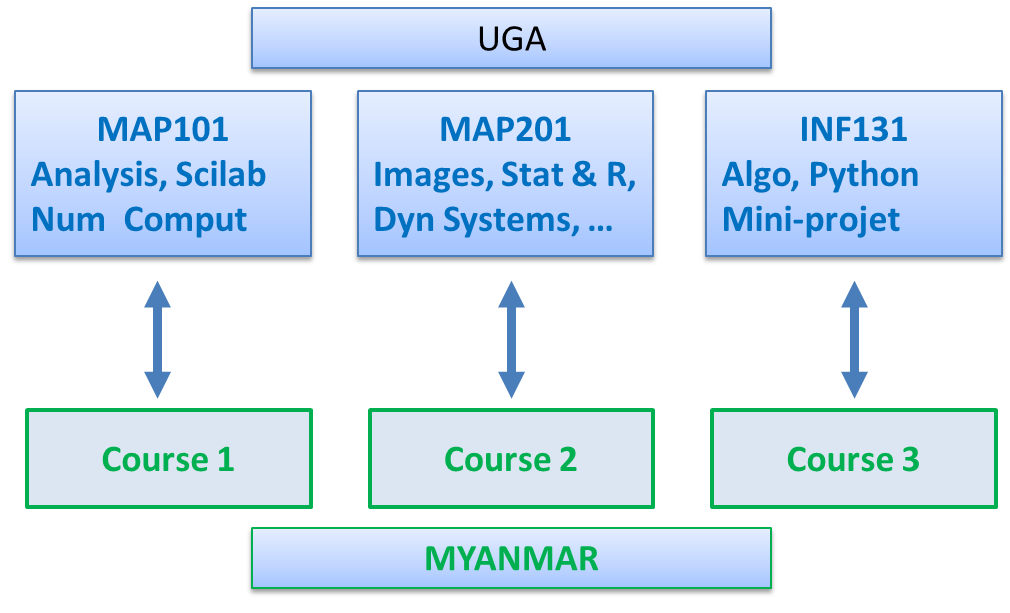
According to our objective, we propose to progressively introduce IT and numerical
mathematics skills into the Myanmar curriculum according to our International Program
in Applied Mathematics
(MIN-Int)
Student and teacher mobilityThe proposal includes one-semester scholarships for Myanmar students at UGA, two-month scholarships for UGA students in Myanmar and one-week visits to UGA for teachers from Myanmar. |
|
|
According to our objective, we propose to proceed as follows.
|
|
