Some information on my Ph.D. Thesis (in french)
Novembre 2005
Titre
Algorithmique en analyse variationnelle et en optimisation semidéfinie
Directeur de thèse
Claude Lemaréchal
Jury
- Jean-Baptiste Hiriart-Urruty, Université Paul Sabatier de Toulouse, Rapporteur
- Anatoli Iouditski, Université Joseph Fourier de Grenoble, Examinateur
- Claude Lemaréchal, INRIA Rhone-Alpes, Directeur de thèse
- Adrian Lewis, Cornell University (USA), Rapporteur
- Yurii Nesterov, Université de Louvain (Belgique), Examinateur
- Francois Oustry, RaisePartner SAS, Examinateur
Résumé
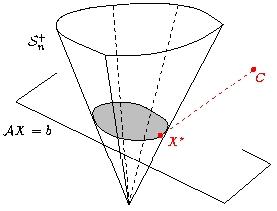
Cette thèse s'inscrit dans le domaine de l'analyse variationnelle et des méthodes numériques d'optimisation, en particulier sur les problèmes pratiques et théoriques mettant en jeu les valeurs propres. La première partie est consacrée à la résolution pratique de problèmes d'optimisation numérique dans l'espace des matrices symétriques, où des contraintes sur les valeurs propres des matrices sont imposées. Plus précisement, nous introduisons des méthodes duales pour calculer la projection sur l'intersection du cône des matrices semidéfinies positives avec un espace affine. Nous présentons alors plusieurs applications de ces méthodes en optimisation combinatoire, en optimisation semidéfinie et en finance. Dans une seconde partie, plus théorique, nous étudions les fonctions non-différentiables qui ont une structure similaire à celle de la fonction valeur propre maximale d'une matrice symétrique. Pour ces fonctions, nous établissons en particulier les liens entre les méthodes de Newton nées de l'analyse convexe moderne, les méthodes de Newton géométriques et les méthodes de type Newton de l'optimisation avec contraintes.