SHOC

SHOC

Hybrid Optimal Control

Optimal control of Hybrid Ordinary Differential Systems

[Presentation]

[Papers]

[Code]

[Contacts]

[Presentation]

This project consists in providing generic algorithms with both symbolic and numerical modules to solve nonlinear optimal control problems.

We consider a general nonlinear dynamical system which state is described by the solution of the following ODE:

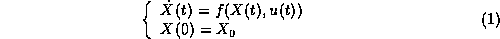
We want to present a generic algorithm for controlling the system (1) from an initial state X₀ at time t=0 to a final state X_f at unspecified time t_f using the admissible control functions u that take values in a convex and compact polyhedral set U_mof R^m, in such a way that:

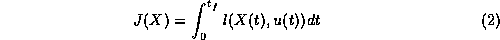
is minimized. The polytope U_m is defined as the convex hull of its vertices:

Affine

We first consider general linear systems. The system (1) is replaced by the following one: X'(t)=AX(t) + Bu(t). We then provide a generic algorithm with both symbolic and numerical modules. Especially we propose new algorithm under-approximating the controllable domain in view of its analytical resolution in the context of singular subarcs. New efficient methods computing a block Kalman canonical decomposition and the optimal solutions are also presented.

Jean-Guillaume Dumas

Hybridization

Our approach is to use hybrid systems to solve this problem: the complex dynamic is replaced by piecewise affine approximations which allow an analytical resolution. The sequence of affine models then forms a sequence of states of a hybrid automaton. Given an optimal sequence of states, we are then able to traverse the automaton till the target, locally insuring the optimality.

[Papers]

For further informations about this work, have a look at:

Piecewise Affine Systems Controllability and Hybrid Optimal Control (ps, pdf)
Aude Rondepierre
ICINCO'05: International Conference on Informatics in Control, Automation and Robotics, September 2005.
Algorithms for Hybrid Optimal Control. Symbolic/Numeric Control of Affine Dynamical Systems.
Aude Rondepierre and Jean-Guillaume Dumas
ISSAC '05: International Symposium on Symbolic and Algebraic Computation, July 2005.

Algorithms for Hybrid Optimal Control.
Aude Rondepierre and Jean-Guillaume Dumas
Rapport de Recherche IMAG-ccsd-00004191, arXiv math.OC/0502172. Février 2005.

Contrôle optimal et algorithme de calcul des trajectoires.

Technical report. IMAG, September 2004

[Source Code]

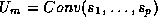
You can also download our source code:

Dimension 2, a first step towards generic algorithms (src, preview), Kevin Hamon.

X'(t)=Bu(t).

In any dimension (src)

Available in this library:

Geometric tools for polytope manipulation.
Hybrid computation: modelisation of nonlinear systems by hybrid systems.
Controllability.
Optimal solutions computation (in progress).

(Full description and user's guide soon available)

To run it, you need:

Maple at least 8.0
Qhull

[Contacts]

Aude RONDEPIERRE
Laboratoire de Modélisation et Calcul
B.P. 53 -- 51, av. des Mathématiques,
38041 Grenoble, France.
Aude.Rondepierre@imag.fr
http://ljk.imag.fr/membres/Aude.Rondepierre

Jean-Guillaume DUMAS
Laboratoire de Modélisation et Calcul
B.P. 53 -- 51, av. des Mathématiques,
38041 Grenoble, France
Jean-Guillaume.Dumas@imag.fr
http://membres-ljk.imag.fr/Jean-Guillaume.Dumas