Calcul de 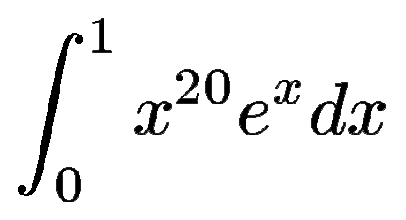 :
:
Récurrence croissante (simple precision) : 6986658816.00000000000000000000
Récurrence croissante (double precision) : 268.20263223784172623709
Récurrence décroissante (simple precision), m0=30 : 0.12380383163690567017
Récurrence décroissante (double precision), m0=30 : 0.12380383076256917807
Récurrence décroissante (simple precision), m0=40 : 0.12380383163690567017
Récurrence décroissante (double precision), m0=40 : 0.12380383076256995523
Trapèzes (double precision), N=100 : 0.12427922672918453872
Trapèzes (double precision), N=1000 : 0.12380858772541204760
Trapèzes (double precision), N=10000 : 0.12380387833249888174
Trapèzes (double precision), N=100000 : 0.12380383123826931013
Simpson (double precision), N=100 : 0.12380390658679736593
Simpson (double precision), N=1000 : 0.12380383077015941207
Simpson (double precision), N=10000 : 0.12380383076257073238
Simpson (double precision), N=100000 : 0.12380383076257016339
Série (double precision), N=10 : 0.12380382102189725624
Série (double precision), N=15 : 0.12380383076254733443
Série (double precision), N=17 : 0.12380383076256987196
Série (double precision), N=18 : 0.12380383076256994135
Série (double precision), N=19 : 0.12380383076256994135
Série (double precision), N=20 : 0.12380383076256994135
Le programme C++.
Le résultat avec 50 chiffres demandés, par maple : 0.1238038307625699486913961699583
[ Polytech'Grenoble
| RICM
| Méthodes
Numériques ]
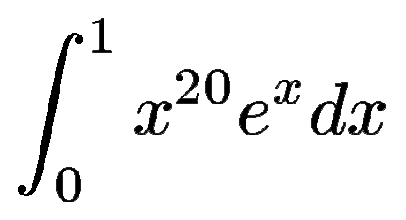 :
: