Section : Les objets du calcul formel
Avant :
Développer et simplifier
Après : Listes, séquences, ensembles
De nombreuses fonctions sont déjà définies dans Xcas, en
particulier les fonctions classiques. Les plus courantes figurent dans
le tableau ci-après; pour les autres, voir le menu Math.
| Fonctions classiques |
abs |
valeur absolue |
round |
arrondi |
floor |
partie entière (plus grand entier 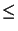 ) ) |
ceil |
plus petit entier 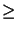 |
abs |
module |
arg |
argument |
conj |
conjugué |
sqrt |
racine carrée |
exp |
exponentielle |
log |
logarithme naturel |
ln |
logarithme naturel |
log10 |
logarithme en base 10 |
sin |
sinus |
cos |
cosinus |
tan |
tangente |
asin |
arc sinus |
acos |
arc cosinus |
atan |
arc tangente |
sinh |
sinus hyperbolique |
cosh |
cosinus hyperbolique |
tanh |
tangente hyperbolique |
asinh |
argument sinus hyperbolique |
acosh |
argument cosinus hyperbolique |
atanh |
argument tangente hyperbolique |
Pour créer une nouvelle fonction, il faut la déclarer à l'aide
d'une expression contenant la variable.
Par exemple l'expression 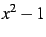 est
définie par
est
définie par x^2-1. Pour la transformer en la fonction 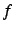 qui
à
qui
à 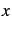 associe
associe 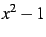 , trois possibilités existent :
, trois possibilités existent :
f(x):= x^2-1
f:=x->x^2-1
f:=unapply(x^2-1,x)
f(2); f(a^2)
Si f est une fonction d'une variable et E est une
expression, f(E) est une autre expression.
Il est essentiel de ne pas confondre fonction et expression.
Si on définit : E:=x^2-1, alors la variable E
contient l'expression 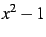 . Pour avoir la valeur de cette
expression en
. Pour avoir la valeur de cette
expression en 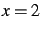 il faut
écrire
il faut
écrire subst(E,x=2) et non E(2)
car E n'est pas une fonction.
Lorsqu'on définit une fonction,
le membre de droite de l'affectation n'est pas évalué.
Ainsi l'écriture E:=x^2-1; f(x):=E
définit la fonction
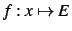 .
Par contre
.
Par contre E:= x^2-1; f:=unapply(E,x) définit bien la
fonction
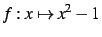 .
.
On peut ajouter et multiplier des fonctions,
par exemple f:=sin*exp. Pour composer des fonctions, on utilise
l'opérateur @ et pour composer plusieurs fois une fonction
avec elle-même, on utilise l'opérateur @@.
f:=x->x^2-1
f1:=f@sin
f2:=f@f
f3:=f@@3
f1(a)
f2(a)
f3(a)
On peut définir des fonctions de plusieurs variables à valeurs dans
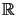 comme
comme f(x,y):=x+2*y et des fonctions de plusieurs
variables à valeurs dans
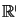 par exemple
par exemple f(x,y):=(x+2*y,x-y)
Section : Les objets du calcul formel
Avant : Développer et simplifier
Après : Listes, séquences, ensembles
R. De Graeve, B. Parisse, B. Ycart 2006