Section : Vecteurs et matrices
Précédent : Opérations
Suivant : Fonctions

Types de données

Certaines constantes sont prédéfinies, et leur valeur ne peut être modifiée.

Constantes prédéfinies
%pi	3.1415927
%e	2.7182818
%i	$\sqrt{-1}$
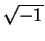%eps	précision machine
%inf	infini
%t	vrai
%f	faux
%s	variable de polynôme

Scilab est un langage faiblement typé. Les variables ne sont pas déclarées, et la même lettre peut désigner un réel, un entier, un polynôme, ou une fonction. Les types existent bien sûr, et peuvent être obtenus par la fonction type. Par défaut, les nombres sont traités comme des réels en double précision. Les calculs ne sont donc pas ``exacts''. La précision machine est donnée par la constante %eps, de l'ordre de 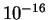$10^{-16}$. Cela ne signifie pas que les nombres inférieurs à %eps ou supérieurs à 1/%eps sont inaccessibles.

help type
%eps
1/%eps
1/%inf
1/0.0000000000000000000000000000000000000003
1/300000000000000000000000000000000000000000
A=[1,2,3;4,5,6;7,8,8]
A/A
A*(1/A)

L'affichage de vecteurs avec de très grandes coordonnées réserve quelques surprises.

v=2^2^[1:5]
v=2^2^[1:6]       // etonnant non ?
v(1:5)            // le calcul etait correct
v=2^2^[1:10]
log(v)./log(2) 
2^[1:10]

A part les réels, les entrées d'une matrice peuvent être des complexes, des booléens, des polynômes ou des chaînes de caractères. Les booléens sont %t (true) et %f (false) pour les saisies, T et F pour les affichages. Les matrices booléennes sont le résultat d'opérations logiques matricielles (toujours terme à terme). Par exemple, si A et B sont deux matrices (réelles) de même taille, A<B est la matrice des booléens A(i,j)<B(i,j). Les opérateurs and et or peuvent s'appliquer à l'ensemble des éléments d'une matrice booléenne, à ses lignes ou à ses colonnes selon l'option choisie. La commande find(v) retourne la liste des indices des coordonnées ``vraies'' du vecteur booléen v. Si v est une matrice, ses colonnes sont préalablement concaténées. Si A est une matrice et B est une matrice de booléens, la commande A(B) extrait de A les coordonnées correspondant aux indices pour lesquels B est à vrai. Cette propriété, fort utile en programmation, a pour corollaire quelques comportements curieux : ones(B) retournera une matrice de même taille que B, mais rand(B) retourne un message d'erreur. La fonction bool2s transforme des booléens en 0 ou 1.

x=rand(2,10)
b=x<0.5
bool2s(b)
and(b)
and(b,"c")
and(b,"r")
or(b,"r")
b1=b(1,:); b2=b(2,:);
b1 & b2
b1 | b2
find(b1)
y=[1:10]
y(b1)
A=[1,2,3;4,5,6;7,8,9]
x=[%t,%f,%t]
A(x,x)
A(~x,x)
B=rand(3,3)<0.5
A(B)

Opérateurs logiques
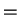==	$=$	~	non
<	$<$	>	$>$
<=	$\leq$	>=	$\geq$
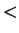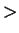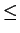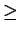&	et	|	ou

Les complexes sont définis à l'aide de la constante %i (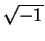$\sqrt{-1}$) ou bien en affectant sqrt(-1) à une nouvelle variable. A noter que par défaut A' est la transposée conjuguée de A. La transposée non conjuguée est A.'. Les fonctions classiques appliquées à un complexe donnent toujours un résultat unique, même si mathématiquement elles ne sont pas définies de façon unique (racine carrée, logarithme, puissances).

A=[1,2;3,4]+%i*[0,1;2,3]
real(A)
imag(A)
conj(A)
A'
A.'
abs(A)
phasemag(A)
i=sqrt(-1)
%i*i
A*i
%e^(%i*%pi)
x=log(%i)
exp(x)
x=%i^(1/3)
x^3

Complexes
real	partie réelle
imag	partie imaginaire
conj	conjugué
abs	module
phasemag	argument (en degrés)

Les polynômes et les fractions rationnelles constituent un type de données particulier. On peut construire un polynôme comme résultat d'opérations sur d'autres polynômes. Il existe par défaut un polynôme élémentaire, %s. On peut construire un polynôme d'une variable quelconque à l'aide de la fonction poly, en spécifiant soit ses racines (par défaut), soit ses coefficients. Les fractions rationnelles sont des quotients de polynômes. Par défaut, Scilab effectue automatiquement les simplifications qu'il reconnaît.

apropos poly
help poly
v=[1,2,3]
p1=poly(v,"x")
roots(p1)
p2=poly(v,"x","c")
coeff(p2)
p1+p2
p3=1+2*%s-3*%s^2
p1+p3                  // erreur : variables differentes
p4=(%s-1)*(%s-2)*(%s-3)
p3/p4

Polynômes
poly(v,"x")	polynôme dont les racines sont les éléments de v
poly(v,"x","c")	polynôme dont les coefficients sont les éléments de v
inv_coeff(v)	idem
coeff(P)	coefficients du polynôme P
roots(P)	racines du polynôme P
factors	facteurs irréductibles réels d'un polynôme
horner	évaluation d'un polynôme

Les chaînes de caractères, encadrées par des doubles côtes ("..."), permettent de définir des expressions mathématiques, interprétables ensuite comme des commandes à exécuter ou des fonctions à définir. Elles servent aussi d'intermédiaire pour des échanges de données avec des fichiers. On peut donc transformer et formater des nombres en chaînes de caractères (voir apropos string).

expression=["x+y","x-y"]     // matrice de 2 chaines de caracteres
length(expression)           // longueurs des 2 chaines
size(expression)             // taille de la matrice 
part(expression,2)           // deuxieme caractere de chaque chaine
expression(1)+expression(2)  // concatenation des deux chaines
x=1; y=2;
evstr(expression)
x=1; instruction="y=(x+1)^2"
execstr(instruction)
y
deff("p=plus(x,y)","p=x+y")
plus(1,2)
plus(2,3)

Chaînes de caractères
evstr	évaluer une expression
deff	définir une fonction
execstr	exécuter une instruction
length	longueur
part	extraire
+	concaténer
string	transformer en chaîne

Section : Vecteurs et matrices
Précédent : Opérations
Suivant : Fonctions