Une mise en garde de Cauchy

En 1822, Cauchy publie au Bulletin de la Société Philomatique «Sur le développement des fonctions en séries et sur l'intégration des équations différentielles ou aux différences partielles». En voici les premières lignes.

Pour découvrir et démontrer les propriétés les plus remarquables des fonctions, on a souvent employé leur développement en séries, ou suites infinies, c'est-à-dire composées d'un nombre infini de termes ;

[...]

Toutefois, en remplaçant des fonctions par des séries, on suppose implicitement qu'une fonction est complètement caractérisée par un développement composé d'un nombre infini de termes, au moins tant que ces termes obtiennent des valeurs finies. Par exemple, lorsqu'on substitue à la fonction $f(x)$ la série de MacLaurin, et que l'on écrit en conséquence

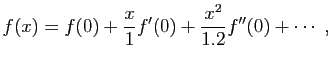$$f(x)=f(0)+\frac{x}{1}f'(0)+\frac{x^2}{1.2}f''(0)+\cdots\;,$$ (1)

on suppose qu'à un système donné de valeurs finies des quantités

$$f(0) ,\;f'(0) ,\;f''(0) \;\ldots$$

correspond toujours une valeur unique de la fonction $f(x)$. Considérons pour fixer les idées, le cas le plus simple, celui où les quantités
$f(0), f'(0), f''(0),\ldots$ s'évanouissent toutes à la fois. Dans cette hypothèse on devra, ce semble, conclure de l'équation (1) que la fonction $f(x)$ s'évanouit elle-même. Néanmoins cette conclusion peut n'être pas exacte. En effet, si on prend

$$f(x)=\mathrm{e}^{-\frac{1}{x^2}}\;,$$

on trouvera

$$f(0)=0 ,\;f'(0)=0 ,\; f''(0)=0 , \ldots$$

[...]

Il suit de ces remarques qu'à une seule série, même convergente, correspond une infinité de fonctions différentes les unes des autres. Il n'est donc pas permis de substituer indistinctement les séries aux fonctions, et pour être assuré de ne commettre aucune erreur, on doit limiter cette substitution au cas où les fonctions, étant développables en séries convergentes, sont équivalentes aux sommes de ces séries. Sous toute autre hypothèse, les séries ne peuvent être employées avec une entière confiance qu'autant qu'elles se trouvent réduites à un nombre fini de termes, et complétées par des restes dont on connaît des valeurs exactes ou approchées.

Et dire que, depuis presque deux siècles, c'est toujours le même contre-exemple que l'on sert aux étudiants !