-
 Toute matrice admet au moins une valeur propre, réelle ou complexe.
Toute matrice admet au moins une valeur propre, réelle ou complexe.
-
 Toute matrice admet une infinité de vecteurs propres, à
coordonnées réelles ou complexes.
Toute matrice admet une infinité de vecteurs propres, à
coordonnées réelles ou complexes.
 Toute matrice réelle
Toute matrice réelle 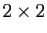 admet une valeur propre réelle.
admet une valeur propre réelle.
-
 Toute matrice réelle
Toute matrice réelle 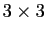 admet une valeur propre réelle.
admet une valeur propre réelle.
 Toute matrice réelle
Toute matrice réelle 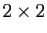 admet un vecteur propre à
coordonnées réelles.
admet un vecteur propre à
coordonnées réelles.
-
 Toute matrice réelle
Toute matrice réelle 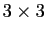 admet un vecteur propre à
coordonnées réelles.
admet un vecteur propre à
coordonnées réelles.
-
 Si une matrice
Si une matrice 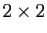 n'est pas diagonalisable dans
n'est pas diagonalisable dans
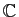 ,
alors elle admet une seule valeur propre.
,
alors elle admet une seule valeur propre.
-
 Si une matrice est triangulaire, alors ses valeurs propres sont ses
éléments diagonaux.
Si une matrice est triangulaire, alors ses valeurs propres sont ses
éléments diagonaux.
 Toute matrice a au moins deux valeurs propres distinctes.
Toute matrice a au moins deux valeurs propres distinctes.
-
 Deux matrices semblables ont les mêmes valeurs propres.
Deux matrices semblables ont les mêmes valeurs propres.
 Les valeurs propres du produit de deux matrices sont les produits des
valeurs propres des deux matrices.
Les valeurs propres du produit de deux matrices sont les produits des
valeurs propres des deux matrices.
-
 Si un vecteur est vecteur propre pour deux matrices, il est vecteur
propre de leur produit.
Si un vecteur est vecteur propre pour deux matrices, il est vecteur
propre de leur produit.
-
 Les valeurs propres d'une matrice et celles de sa transposée sont
les mêmes.
Les valeurs propres d'une matrice et celles de sa transposée sont
les mêmes.
 Les vecteurs propres d'une matrice et ceux de sa transposée sont
les mêmes.
Les vecteurs propres d'une matrice et ceux de sa transposée sont
les mêmes.
 Le produit d'une matrice par un de ses vecteurs propres ne peut pas
être le vecteur nul.
Le produit d'une matrice par un de ses vecteurs propres ne peut pas
être le vecteur nul.
 Si une matrice a toutes ses valeurs propres réelles, alors elle est
diagonalisable.
Si une matrice a toutes ses valeurs propres réelles, alors elle est
diagonalisable.
-
 Si une matrice
Si une matrice 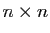 a
a 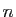 valeurs propres distinctes, alors elle est
diagonalisable.
valeurs propres distinctes, alors elle est
diagonalisable.
 La somme des valeurs propres d'une matrice est égale au produit de
ses éléments diagonaux.
La somme des valeurs propres d'une matrice est égale au produit de
ses éléments diagonaux.
-
 Le produit des valeurs propres d'une matrice est égal à son
déterminant.
Le produit des valeurs propres d'une matrice est égal à son
déterminant.
 La matrice de la rotation vectorielle d'angle
La matrice de la rotation vectorielle d'angle
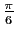 dans le plan admet des valeurs propres réelles.
dans le plan admet des valeurs propres réelles.
-
 La matrice d'une symétrie vectorielle
dans le plan a pour valeurs propres
La matrice d'une symétrie vectorielle
dans le plan a pour valeurs propres 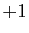 et
et 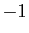 .
.
-
 Si
Si 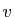 est vecteur propre d'une matrice, alors
est vecteur propre d'une matrice, alors 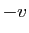 est aussi vecteur
propre de cette matrice.
est aussi vecteur
propre de cette matrice.
 Si
Si 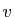 et
et 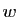 sont vecteurs propres d'une même matrice, alors
sont vecteurs propres d'une même matrice, alors 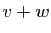 est toujours vecteur propre de cette matrice.
est toujours vecteur propre de cette matrice.
![\begin{displaymath}
\left\{
\begin{array}{lcr}
u_{n+1} = u_n - v_n [2ex]
v_{n+1} = u_n+v_n
\end{array}\right.
\end{displaymath}](img666.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales