Le théorème fondamental de la géométrie affine

Toute transformation affine conserve l'alignement et transforme une droite en une droite. On peut se demander si cette propriété caractérise les transformations affines. C'est le cas dans le plan affine réel :

Théorème 7   Toute bijection du plan affine réel sur lui-même qui transforme toute droite en une droite est une transformation affine .

Ce théorème reste vrai dans un espace affine $E$ quelconque, à condition de prendre quelques précautions :

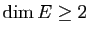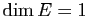1. il faut avoir $\dim E\geq 2$ (si $\dim E=1$, toute bijection de $E$ sur $E$ vérifie trivialement la condition et il est facile de construire des bijections de $E$ sur $E$ qui ne sont pas affines) ;
2. il faut que le corps de base n'admette pas d'autre automorphisme de corps que l'identité (si 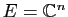$E=\mathbb{C}^n$, l'application qui à 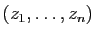$(z_1,\dots,z_n)$ associe 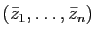$(\bar z_1,\dots,\bar z_n)$ transforme toute droite en une droite, mais n'est pas affine).