Et ignem regunt numeri

«Même le feu est régi par les nombres» : c'est la citation attribuée à Platon que porte en exergue la «Théorie Analytique de la chaleur» de Joseph Fourier (1768-1830). Quel est le problème ?

Lorsque la chaleur est inégalement distribuée entre les différents points d'une masse solide, elle tend à se mettre en équilibre, et passe lentement des parties les plus échauffées dans celles qui le sont moins ; en même temps elle se dissipe par la surface, et se perd dans le milieu ou dans le vide. Cette tendance à une distribution uniforme, et cette émission spontanée qui s'opère à la surface des corps, changent continuellement la température des différents points. La question de la propagation de la chaleur consiste à déterminer quelle est la température de chaque point d'un corps à un instant donné, en supposant que les températures initiales sont connues.

Cette «question de la propagation de la chaleur», Fourier estime l'avoir résolue dès 1807. Si $v(t,x,y,z)$ désigne la température d'un corps au point de coordonnées $(x,y,z)$ et au temps $t$, alors à l'intérieur du corps :

$$\frac{dv}{dt}= \frac{K}{C.D} . \left(\frac{d^2 v}{d x^2}+\frac{d^2 v}{d y^2}+\frac{d^2 v}{d z^2}\right)\;,$$

où $K$ est la conductibilité interne, $D$ la densité et $C$ la chaleur spécifique. Les conditions aux bords, la manière de résoudre numériquement les équations différentielles avec des séries trigonométriques, tout avait été établi, et soigneusement validé par de nombreuses expériences sur des corps de différentes formes. Alors pourquoi son premier mémoire de 1807 n'a-t-il pas été considéré ? Pourquoi sa nouvelle soumission en 1812 a-t-elle été primée, mais curieusement non publiée ?

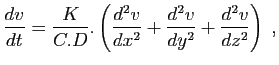
Cette pièce renferme les véritables équations différentielles de transmission de la chaleur, soit à l'intérieur des corps, soit à leur surface ; et la nouveauté du sujet, jointe à son importance, a déterminé la Classe à couronner cet ouvrage, en observant cependant que la manière dont l'auteur parvient à ses équations n'est pas exempte de difficultés, et que son analyse, pour les intégrer, laisse encore quelque choses à désirer, soit relativement à la généralité, soit même du côté de la rigueur.

Une première élection à l'Académie des Sciences est récusée par Louis XVIII (sous la Restauration, ceux qui s'étaient trop marqués du côté de Napoléon n'étaient pas en odeur de sainteté). Candidat à nouveau dans la section de Physique générale, il est réélu et enfin nommé en mai 1817. C'est la consécration ; il réunit ses différents travaux, et la publication en 1822 de la Théorie Analytique de la Chaleur marque son triomphe : 660 pages, dont 21 de discours préliminaire, où profitant de son autorité enfin reconnue, il énonce sa philosophie de la science, au risque de pontifier un tantinet.

Les équations du mouvement de la chaleur, comme celles qui expriment les vibrations des corps sonores, ou les dernières oscillations des liquides, appartiennent à une des branches de la science du calcul les plus récemment découvertes, et qu'il importait beaucoup de perfectionner. Après avoir établi ces équations différentielles, il fallait en établir les intégrales ; ce qui consiste à passer d'une expression commune à une solution propre assujettie à toutes les conditions données. Cette recherche difficile exigeait une analyse spéciale, fondée sur des théorèmes nouveaux dont nous ne pourrions ici faire connaître l'objet. La méthode qui en dérive ne laisse rien de vague, ni d'indéterminé dans les solutions ; elle les conduit jusqu'aux dernières applications numériques, condition nécessaire de toute recherche, sans lesquelles on n'arriverait qu'à des transformations inutiles.

[...]

L'étude de la nature est la source la plus féconde des découvertes mathématiques. Non seulement cette étude, en offrant aux recherches un but déterminé, a l'avantage d'exclure les questions vagues et les calculs sans issue ; elle est encore un moyen assuré de former l'analyse elle-même, et d'en découvrir les éléments qu'il nous importe le plus de connaître, et que cette science doit toujours conserver : ces éléments fondamentaux sont ceux qui se reproduisent dans tous les effets naturels.

Les équations analytiques, ignorées des anciens géomètres, que Descartes a introduites le premier dans l'étude des courbes et des surfaces, ne sont pas restreintes aux propriétés des figures, et à celles qui sont l'objet de la mécanique rationnelle : elles s'étendent à tous les phénomènes généraux. Il ne peut y avoir de langage universel et plus simple, plus exempt d'erreurs et d'obscurités, c'est-à-dire plus digne d'exprimer les rapports invariables des êtres naturels.

Considérée sous ce point de vue, l'analyse mathématique est aussi étendue que la nature elle-même ; elle définit tous les rapports sensibles, mesure les temps, les espaces, les forces, les températures ; cette science difficile se forme avec lenteur, mais elle conserve tous les principes qu'elle a une fois acquis ; elle s'accroît et s'affermit sans cesse au milien de tant de variations et d'erreurs de l'esprit humain.

Son attribut principal est la clarté. Elle n'a point de signes pour exprimer les notions confuses. Elle rapproche les phénomènes les plus divers, et découvre les analogies secrètes qui les unissent. Si la matière nous échappe comme celle de l'air et de la lumière par son extrême ténuité, si les corps sont placés loin de nous, dans l'immensité de l'espace, si l'homme veut connaître le spectacle des cieux pour des époques successives que sépare un grand nombre de siècles, si les actions de la gravité et de la chaleur s'exercent dans l'intérieur du globe solide à des profondeurs qui seront toujours inaccessibles, l'analyse mathématique peut encore saisir les lois de ces phénomènes. Elle nous les rend présents et mesurables, et semble être une faculté de la raison humaine, destinée à suppléer à la brièveté de la vie et à l'imperfection des sens ; et ce qui est plus remarquable encore, elle suit la même marche dans l'étude de tous les phénomènes ; elle les interprète dans le même langage, comme pour attester l'unité et la simplicité du plan de l'univers, et rendre encore plus manifeste cet ordre immuable qui préside à toutes les causes naturelles.

[...]

Les théories nouvelles, expliquées dans notre ouvrage sont réunies pour toujours aux sciences mathématiques, et reposent comme elles sur des fondements invariables ; elles conserveront tous les éléments qu'elles possèdent aujourd'hui, et elles acquerront continuellement plus d'étendue. On perfectionnera les instruments et l'on multipliera les expériences. L'analyse que nous avons formée sera déduite de méthodes plus générales, c'est-à-dire plus simples et plus fécondes, communes à plusieurs stances solides ou liquides, pour les vapeurs et pour les gaz permanents, toutes les qualités spécifiques relatives à la chaleur, et les variations des coefficients qui les expriment. On observera, dans divers lieux du globe, les températures du sol à diverses profondeurs, l'intensité de la chaleur solaire, et ses effets, ou constants ou variables, dans l'atmosphère, dans l'Océan et les lacs ; et l'on connaîtra cette température constante du Ciel, qui est propre aux régions planétaires. La théorie elle-même dirigera toutes ces mesures, et en assignera la précision. Elle ne peut faire désormais aucun progrès considérable qui ne soit fondé sur ces expériences ; car l'analyse mathématique peut déduire des phénomènes généraux et simples l'expression des lois de la nature ; mais l'application spéciale de ces lois à des effets très composés exige une longue suite d'observations exactes.

Fourier revendique hautement l'«étude de la Nature», jusqu'aux «applications numériques, condition nécessaire de toute recherche». Déjà à l'époque, ce n'était pas le point de vue unanime. Voici ce que le jeune Jacobi écrit à Legendre peu après la mort de Fourier :

Il est vrai que M. Fourier avait l'opinion que le but principal des mathématiques était l'utilité publique et l'explication des phénomènes naturels ; mais un philosophe comme lui aurait dû saisir que le but unique de la science, c'est l'honneur de l'esprit humain, et que sous ce titre, une question de nombres vaut autant qu'une question de système du monde.

Après 1822, Fourier écrit encore plusieurs articles sur la chaleur, dont deux consacrés à la température du globe terrestre, dans lesquels la mode actuelle veut voir l'anticipation de l'effet de serre et du réchauffement climatique. L'avènement de l'ordinateur avait déjà fait de la transformée de Fourier un nom commun, le voici promu fer de lance du sauvetage planétaire : quelle revanche !