http://www.mathcurve.com/.
Nous allons essayer de vous donner envie d'en savoir plus, en partant
de l'équation la plus simple possible :
Pour imaginer la surface d'équation ![]() , examinons
d'abord quelques unes de ses sections planes. Nous notons
, examinons
d'abord quelques unes de ses sections planes. Nous notons ![]() la surface et nous considérons
son intersection avec le plan
la surface et nous considérons
son intersection avec le plan ![]() dont nous donnons l'équation,
en fonction d'un paramètre réel
dont nous donnons l'équation,
en fonction d'un paramètre réel ![]() .
.
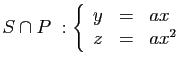 :
: 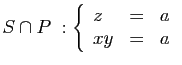 :
: 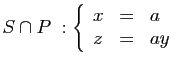 :
: 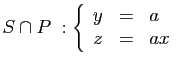 :
: 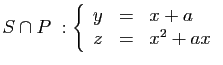 :
: 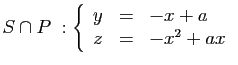 : encore une autre famille de paraboles, orientées vers le bas, dans des plans
orthogonaux aux précédents.
: encore une autre famille de paraboles, orientées vers le bas, dans des plans
orthogonaux aux précédents.
Les surfaces doublement réglées font le bonheur des architectes : on peut couler d'immenses dalles de béton en les armant selon une des deux familles de droites, tout en coffrant le long l'autre famille, ce qui confère à la structure d'excellentes propriétés mécaniques : le toit de la cathédrale de la Sagrada Familia à Barcelone celui du musée océanographique de Valence, sont des portions de paraboloïde hyperbolique. Au fait, vous êtes-vous demandé pourquoi les biscuits d'apéritif de la marque Pringles ont cette forme en selle de cheval plutôt que d'être plats ?
L'hyperboloïde de révolution est un autre exemple de surface doublement réglée. Pour vous en faire une idée, prenez un paquet de tiges rigides (baguettes de mikado, pailles ...) que vous maintenez en son milieu par un élastique. Élargissez ensuite le paquet par en haut et par en bas en penchant les baguettes d'un même angle : vous venez de matérialiser un hyperboloïde de révolution (figure 15). Il est aussi très utilisé en architecture : châteaux d'eau, cheminées de centrale nucléaire...
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales