| (1) |
Nous n'aborderons pas ces questions théoriques, qui dépassent le niveau de ce cours. Toutes les équations différentielles qui seront traitées ont des solutions, et nous le vérifierons au cas par cas.
Il existe de très nombreuses méthodes de résolution formelle des équations différentielles, adaptées chacune à un type particulier d'équation. Elles sont implémentées dans les logiciels de calcul formel comme Xcas. Le but de ce chapitre est de présenter certaines des plus simples de ces méthodes.
Les problèmes différentiels rencontrés dans les
applications n'ont que rarement une solution formelle
explicite. De plus la résolution explicite,
qu'elle produise une solution comme
combinaison de fonctions classiques, sous forme de série entière ou de
transformée de Laplace inverse, ne fait que déplacer le problème
de l'évaluation numérique. Considérons par exemple
![]() . La
solution est immédiate, c'est
. La
solution est immédiate, c'est
![]() .
Mais s'il doit calculer
.
Mais s'il doit calculer
![]() pour
pour
![]() , l'ordinateur utilisera un algorithme d'approximation polynomiale.
Les fonctions classiques peuvent être définies comme des
sommes de séries (exponentielle),
des intégrales (fonction Gamma), ou même des solutions de certaines
équations différentielles (fonctions de Bessel). Dans ce dernier cas
c'est précisément parce que des équations couramment rencontrées
n'avaient pas de solution explicite que l'on a été amené à
baptiser leurs solutions. Pour un ordinateur, toute fonction,
qu'elle soit «explicite» ou non, correspond in fine à un algorithme
de calcul approché : approximation polynomiale, intégration
numérique, ou même résolution numérique d'équation différentielle.
Les méthodes d'approximation numérique ont donc une portée
beaucoup plus générale que les méthodes formelles, mais
nous ne les aborderons pas.
, l'ordinateur utilisera un algorithme d'approximation polynomiale.
Les fonctions classiques peuvent être définies comme des
sommes de séries (exponentielle),
des intégrales (fonction Gamma), ou même des solutions de certaines
équations différentielles (fonctions de Bessel). Dans ce dernier cas
c'est précisément parce que des équations couramment rencontrées
n'avaient pas de solution explicite que l'on a été amené à
baptiser leurs solutions. Pour un ordinateur, toute fonction,
qu'elle soit «explicite» ou non, correspond in fine à un algorithme
de calcul approché : approximation polynomiale, intégration
numérique, ou même résolution numérique d'équation différentielle.
Les méthodes d'approximation numérique ont donc une portée
beaucoup plus générale que les méthodes formelles, mais
nous ne les aborderons pas.
Toujours au prix d'une augmentation de la dimension, on peut ramener une
équation d'ordre ![]() à une équation d'ordre
à une équation d'ordre ![]() . Il suffit pour
cela de poser :
. Il suffit pour
cela de poser :
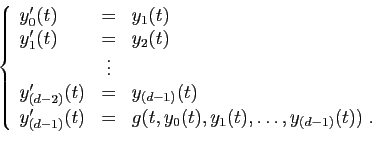
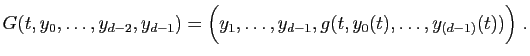
Considérons une équation différentielle d'ordre ![]() dans
dans
![]() ,
homogène en temps :
,
homogène en temps :
Exemple 1 (figure 1) :
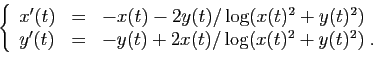
Exemple 2 (figure 2) :
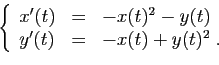
Nous allons chercher à résoudre certaines équations
d'ordre ![]() , dont les fonctions inconnues seront
des fonctions de
, dont les fonctions inconnues seront
des fonctions de
![]() dans
dans
![]() .
.
Exemple 3 (figure 3) :
Exemple 4 (figure 4) :
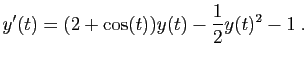
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales