-
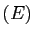 est une équation linéaire homogène du premier ordre.
est une équation linéaire homogène du premier ordre.

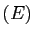 a une solution unique.
a une solution unique.
 La fonction nulle (
La fonction nulle (
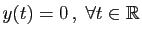 ) est solution de
) est solution de 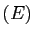 sur
sur
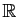 .
.
-
 La fonction nulle est solution de
La fonction nulle est solution de 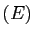 sur
sur
![$ ]0,+\infty[ $](img303.gif) .
.
 Toute solution de
Toute solution de 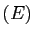 est définie sur
est définie sur
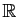 .
.
 Pour tout
Pour tout
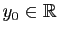 ,
, 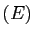 admet une solution unique telle que
admet une solution unique telle que
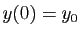 .
.
-
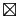 Pour tout
Pour tout
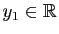 ,
, 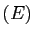 admet une solution unique telle que
admet une solution unique telle que
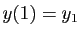 , définie sur
, définie sur
![$ ]0,+\infty[ $](img303.gif) .
.

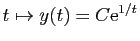 est solution de
est solution de 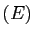 , pour tout
, pour tout
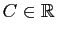 , sur
l'intervalle
, sur
l'intervalle
![$ ]0,+\infty[ $](img303.gif) .
.
-
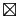
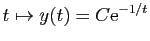 est solution de
est solution de 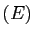 , pour tout
, pour tout
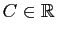 , sur
l'intervalle
, sur
l'intervalle
![$ ]-\infty,0[ $](img302.gif) .
.
-
 La fonction
La fonction 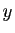 définie par
définie par
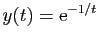 si
si 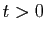 ,
,
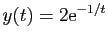 si
si 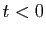 et
et 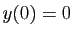 ,
est indéfiniment dérivable sur
,
est indéfiniment dérivable sur
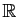 .
.
 La fonction
La fonction 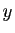 de la question précédente est solution de
de la question précédente est solution de 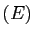 sur
sur
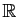 .
.
-
 La fonction
La fonction 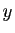 définie par
définie par
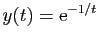 si
si 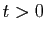 et
et
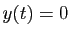 sinon, est solution de
sinon, est solution de 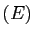 sur
sur
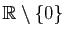 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales