Vous aurez été prévenu5 ! On considère la
suite
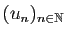 définie par
définie par
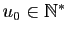 et pour tout
et pour tout
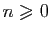 :
:
Si 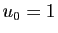 , alors
, alors 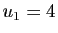 ,
, 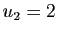 et
et 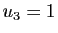 : est-ce le seul cycle ?
Est-il vrai que la suite boucle sur
: est-ce le seul cycle ?
Est-il vrai que la suite boucle sur 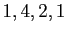 quel que soit son point de
départ ? Personne n'a jamais répondu à cette question, et ce n'est
pas faute d'avoir essayé. Cette suite apparaît parfois dans la
littérature sous le nom de «suite de Syracuse», non pas
qu'elle ait un quelconque rapport avec Archimède, mais à cause du
temps qu'elle a fait perdre aux mathématiciens de l'Université de
Syracuse, dans l'état de New York au début des années 50.
Certains ont prétendu que le problème
avait été inventé spécialement pour faire baisser la
productivité des départements de mathématiques aux USA pendant
la guerre froide. L'auteur du problème, Lothar Collatz, s'en
défend : il avait pensé à cette suite alors qu'il était
encore étudiant à la fin des années 30. Ce type d'énoncé
très simple a toujours fasciné les mathématiciens, et faisait
dire à Paul Erdos, pourtant orfèvre en la matière : «
Mathematics is not yet ripe enough for such questions».
Malgré nos avertissements, vous avez sans doute déjà essayé
quelques valeurs de tête. Un conseil : utilisez plutôt Xcas !
quel que soit son point de
départ ? Personne n'a jamais répondu à cette question, et ce n'est
pas faute d'avoir essayé. Cette suite apparaît parfois dans la
littérature sous le nom de «suite de Syracuse», non pas
qu'elle ait un quelconque rapport avec Archimède, mais à cause du
temps qu'elle a fait perdre aux mathématiciens de l'Université de
Syracuse, dans l'état de New York au début des années 50.
Certains ont prétendu que le problème
avait été inventé spécialement pour faire baisser la
productivité des départements de mathématiques aux USA pendant
la guerre froide. L'auteur du problème, Lothar Collatz, s'en
défend : il avait pensé à cette suite alors qu'il était
encore étudiant à la fin des années 30. Ce type d'énoncé
très simple a toujours fasciné les mathématiciens, et faisait
dire à Paul Erdos, pourtant orfèvre en la matière : «
Mathematics is not yet ripe enough for such questions».
Malgré nos avertissements, vous avez sans doute déjà essayé
quelques valeurs de tête. Un conseil : utilisez plutôt Xcas !
syracuse(a):={
local u,s;
u:=a; s:=u;
while (u!=1)
{
if (irem(u,2)==0)
{u:=iquo(u,2)}
else
{u:=3*u+1}
s:=s,u;
}
return(s);
};
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![$\displaystyle u_{n+1}=\left\{\begin{array}{ll}
3u_n+1&\mbox{si $u_n$ est impair...
...2ex]
\displaystyle{\frac{u_n}{2}}&\mbox{si $u_n$ est pair.}
\end{array}\right.
$](img309.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales