Vous êtes-vous demandé comment fait votre calculette pour retourner
instantanément avec 10 chiffres de précision n'importe quelle valeur
d'une fonction usuelle ? À la lecture de ce qui précède, vous êtes
peut-être tenté de croire à une approximation polynomiale,
calculée par la méthode des différences. Non : votre calculette
utilise probablement l'algorithme CORDIC (pour Coordinate
Rotation Digital Computer), inventé
par J. Volder en 1959, et généralisé par J. Walther en
19715.
Voici le principe, pour les fonctions trigonométriques.
Soit à calculer
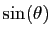 et
et
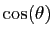 , pour un certain angle
, pour un certain angle 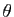 .
L'idée consiste à approcher
.
L'idée consiste à approcher 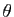 par la suite
par la suite
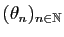 , définie par
, définie par
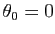 et
pour tout
et
pour tout
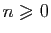 :
:
La série de terme général
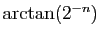 est convergente.
De plus, pour tout
est convergente.
De plus, pour tout
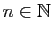 :
:
Démontrez-le, et déduisez-en que la suite
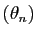 converge
vers
converge
vers 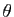 , pour tout
, pour tout 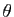 compris
entre deux valeurs extrêmes :
compris
entre deux valeurs extrêmes :
Ce n'est pas une limitation gênante : comme vous le savez, on peut toujours
se ramener à un angle compris entre 0 et 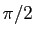 ,
quitte à changer ensuite
le signe du résultat.
,
quitte à changer ensuite
le signe du résultat.
n=[1:100]; sum(atan(2^(-n)))/%pi
Les angles
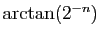 sont fixes : ils peuvent être
tabulés et mémorisés. Peu de valeurs sont nécessaires, car pour
sont fixes : ils peuvent être
tabulés et mémorisés. Peu de valeurs sont nécessaires, car pour 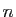 assez grand,
assez grand, 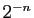 est une bonne approximation de
est une bonne approximation de
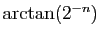 .
.
d=2^(-[0:10]); atan(d)-d
Notons 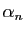 l'angle
l'angle
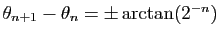 .
Les valeurs approchant le cosinus et le sinus de
.
Les valeurs approchant le cosinus et le sinus de 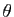 sont
sont
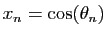 ,
,
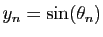 . Le vecteur de coordonnées
. Le vecteur de coordonnées
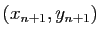 se déduit
du précédent par une rotation d'angle
se déduit
du précédent par une rotation d'angle
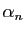 (d'où le nom de l'algorithme) :
(d'où le nom de l'algorithme) :
Pour tout
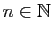 , posons
, posons
Posons
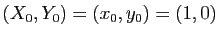 , et pour tout
, et pour tout
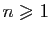 ,
,
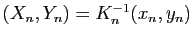 . Il vient :
. Il vient :
La puissance de l'algorithme réside dans cette formule
de récurrence : elle ne comporte que des additions,
et des multiplications par
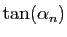 . Or
par définition de
. Or
par définition de 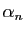 ,
,
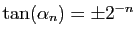 .
Multiplier par
.
Multiplier par
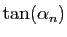 en arithmétique binaire, c'est
décaler la virgule de
en arithmétique binaire, c'est
décaler la virgule de 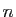 places, et éventuellement inverser
le bit de signe. Le calcul de
places, et éventuellement inverser
le bit de signe. Le calcul de 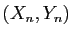 est donc peu coûteux.
Pour revenir à
est donc peu coûteux.
Pour revenir à 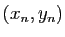 , il faut
multiplier par
, il faut
multiplier par 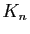 : les valeurs de
: les valeurs de 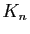 sont fixes et peuvent être mémorisées.
Peu de valeurs sont nécessaires car le produit
converge vite.
sont fixes et peuvent être mémorisées.
Peu de valeurs sont nécessaires car le produit
converge vite.
cumprod(cos(atan(2^(-[0:15]))))
Voici en Scilab le calcul de 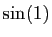 et
et
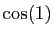 (non optimisé bien sûr).
(non optimisé bien sûr).
theta=1; tn=0; v=[1;0]; V=[]; n=40;
for i=0:n,
s=sign(theta-tn); tn=tn+s*atan(2^(-i));
b=s*2^(-i); M=[1,-b;b,1]; v=M*v; V=[V,v];
end;
K=cumprod(cos(atan(2^(-[0:n])))); sc=V.*[K;K]
sc-[cos(theta);sin(theta)]*ones(1,n+1)
Pour les autres fonctions usuelles, il faut définir
une autre notion de «rotation», mais le principe
reste le même : une récurrence linéaire peu coûteuse,
éventuellement suivie
d'une multiplication par des valeurs mémorisées.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et
![]() , pour un certain angle
, pour un certain angle ![]() .
L'idée consiste à approcher
.
L'idée consiste à approcher ![]() par la suite
par la suite
![]() , définie par
, définie par
![]() et
pour tout
et
pour tout
![]() :
:
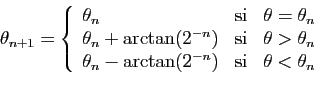
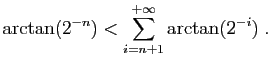

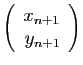
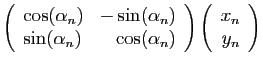
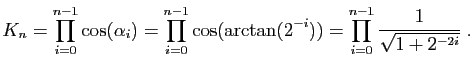
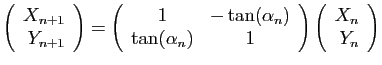
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales