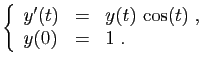Equations différentielles

La fonction ode est en fait un environnement qui donne accès à la plupart des méthodes numériques classiques pour la résolution des équations différentielles ordinaires (voir help ode).

À titre d'exemple nous commençons par le problème de Cauchy en dimension 1 suivant :

$$\left\{ \begin{array}{lcl} y'(t) &=& y(t) \cos(t)\;,\ y(0) &=& 1\;. \end{array} \right.$$

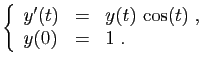La solution explicite est $y(t)=\exp(\sin(t))$. La résolution numérique par ode est très stable.

deff("yprim=f(t,y)","yprim=y*cos(t)")
t0=0; y0=1; t=[0:0.01:10];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(sin(t))))     // l'erreur est tres faible
t0=0; y0=1; t=[0:0.1:100];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(sin(t))))     // l'erreur reste tres faible

La situation n'est pas toujours aussi favorable. Considérons par exemple $y(t)=\exp(t)$, solution du problème de Cauchy suivant.

$$\left\{ \begin{array}{lcl} y'(t) &=& y(t)\;,\ y(0) &=& 1\;. \end{array} \right.$$

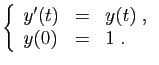deff("yprim=f(t,y)","yprim=y")
t0=0; y0=1; t=[0:0.01:10];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(t)))          // l'erreur est raisonnable
t0=0; y0=1; t=[0:0.1:100];
sol=ode(y0,t0,t,f);
max(abs(sol-exp(t)))          // l'erreur est enorme

Voici en dimension 2 la résolution d'un système différentiel de Lotka-Volterra, avec superposition de la trajectoire calculée et du champ de vecteurs défini par le système (figure 8).

//
// definition du systeme 
//
deff("yprim=f(t,y)",..
    ["yprim1=y(1)-y(1)*y(2)";..
     "yprim2=-2*y(2)+2*y(1)*y(2)";..
     "yprim=[yprim1;yprim2]"])
//
// champ de vecteurs
//
xmin=0; xmax=3; ymin=0; ymax=4;
fx=xmin:0.3:xmax; fy=ymin:0.3:ymax;
clf()
fchamp(f,1,fx,fy)
//
//resolution du systeme
//
t0=0; tmax=8; pas=0.1
t=t0:pas:tmax;
y0=[2; 2];
sol=ode(y0,t0,t,f);
//
// trace de la trajectoire et point initial
//
plot2d(y0(1),y0(2),style=-3)
plot2d(sol(1,:),sol(2,:),style=5)

Figure 8: Résolution d'un système de Lotka-Volterra par ode, représentation de plusieurs solutions et du champ de vecteurs.