Probabilités et Statistique avec R

Lois usuelles et génération de données aléatoiresLe logiciel R permet d'effectuer des calculs avec toutes les lois de probabilité usuelles, et aussi de simuler des échantillons issus de ces lois. Le tableau suivant résume les différentes lois implémentées dans R.

Loi	appelation R	Arguments
bêta	`beta`	`forme 1, forme 2`
binomiale	`binom`	`size, prob`
chi deux	`chisq`	`df` (degrés de liberté)
uniforme	`unif`	`min, max`
exponentielle	`exp`	`rate`
Fisher	`f`	`df1, df2`
gamma	`gamma`	`forme, echelle`
géometrique	`geom`	`prob`
hypergéometrique	`hyper`	`m, n, k` (taille échantillon)
binomiale négative	`nbinom`	`size, prob`
normale	`norm`	`mean, sd`
Poisson	`pois`	`lambda`
Student	`t`	`df`
Weibull	`weibull`	`forme, echelle`

Pour certaines lois, les paramètres ont des valeurs par défaut : parmi les plus utilisées, la loi uniforme unif porte par défaut sur l'intervalle

, et la loi normale norm est centrée réduite par défaut.

Pour effectuer un calcul avec une de ces lois, il suffit d'utiliser comme fonction l'une des appellations R ci-dessus avec le préfixe d pour une densité, p pour une fonction de répartition, q pour une fonction quantile et r pour un tirage aléatoire. Voici quelques exemples :

x <- rnorm(100)          # 100 tirages, loi N(0,1)
w <- rexp(1000, rate=.1) # 1000 tirages, loi exponentielle
dpois(0:2, lambda=4)     # probablités de 0,1,2 pour la loi Poisson(4)
pnorm(12,mean=10,sd=2)   # P(X < 12) pour la loi N(10,4)
qnorm(.75,mean=10,sd=2)  # 3ème quartile de  la loi N(10,4)

Voici à titre d'exemple une utilisation de la génération de nombres aléatoires pour évaluer une intégrale numérique (Méthode de Monte Carlo). Soit une fonction réelle intégrable sur un intervalle . Nous souhaitons calculer une valeur approchée de $I=\int_a^b g(x) dx$ . Générons un échantillon $(x_1, x_2, \dots, x_n)$ de taille de loi uniforme sur et calculons :

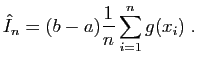
$\displaystyle \hat{I}_n = (b-a) \frac{1}{n} \sum_{i=1}^n g(x_i)\;.$

La loi des grands nombres assure la convergence presque sûre, quand

tend vers l'infini, de $\hat{I}_n$ vers

, et donc pour

grand, $\hat{I}_n$ est une approximation de

(moins bonne, certes, que celle obtenue par quadrature numérique). Considérons le calcul de l'intégrale $\int_0^{\pi/2} \sin(x) \exp(-x^2) dx$ par simulation de Monte Carlo, et son calcul numérique par la fonction integrate :

u <- runif(1000000, min=0, max=pi/2)
I <- pi/2* mean(sin(u)*exp(-u^2)) 
f<-function(x){sin(x)*exp(-x^2)}
integrate(f,lower=0,upper=pi/2)

Tracés de densités et de fonctions de répartitions

Des tracés de densités de probabilité ou de fonctions de répartition de lois diverses peuvent s'obtenir à l'aide de la function plot(). Ainsi par exemple pour tracer la densité (répartition des masses) d'une loi binomiale avec and , reproduite dans la figure 13, on exécute dans R :

x <- 0:10
y <- dbinom(x, size=10, prob=.25)    # évalue les probas
{plot(x, y, type = "h", lwd = 30, 
      main = "Densité Binomiale avec \n n 
      = 10, p = .25", ylab = "p(x)", lend ="square")}

**Figure 13:** Loi binomiale $\mathcal {B}(10,0.25)$ .
$\includegraphics[width=7cm]{dens1}$

Pour cet exemple, nous avons d'abord créé le vecteur x contenant les entiers allant de 0 à 10. Nous avons ensuite calculé les probabilités qu'une variable de loi binomiale prenne chacune de ces valeurs, par dbinom. Le type de tracé est spécifié avec l'option type=h (lignes verticales d'un diagramme en bâtons), épaissies grâce à l'option lwd=30. L'option lend ="square" permet de tracer des barres rectangulaires. Nous avons ensuite ajouté des légendes.

Pour tracer des densités de lois absolument continues ou des fonctions de répartitions de celles-ci, on peut utiliser la fonction curve(). Par exemple, le tracé de la densité d'une loi Gaussienne centrée réduite sur l'intervalle s'obtient avec la commande curve(dnorm(x), from = -3, to = 3) qui réalise la figure 14.

**Figure 14:** Densité de la loi $\mathcal {N}(0,1)$
$\includegraphics[width=6cm]{dens2}$

alors que la commande curve(pnorm(x, mean=10, sd=2), from = 4, to = 16) produit le tracé de la fonction de répartition d'une loi $\mathcal {N}(10,4)$ sur l'intervalle

**Figure 15:** Fonction de répartition de la loi $\mathcal {N}(10,4)$
$\includegraphics[width=6cm]{dens3}$

Notons que la fonction curve() permet également de superposer une courbe sur un autre tracé (dans ce cas il est inutile de spécifier from et to). Essayons par exemple de comparer l'histogramme des fréquences des valeurs obtenues par un tirage de 1000 nombres selon la loi $\mathcal {N}(0,1)$ avec la densité de la loi $\mathcal {N}(0,1)$ :

 simu <- rnorm(1000)
 {hist(simu, prob=T, breaks="FD", 
       main="Histogramme de 1000 tirages N(0,1)")}
 curve(dnorm(x), add=T)

qui donne la figure 16.

**Figure 16:** Histogramme d'un échantillon de taille 1000 de la loi $\mathcal {N}(0,1)$ .
$\includegraphics[width=6cm]{dens4}$

La fonction sample permet d'extraire des échantillons d'un ensemble fini quelconque, avec ou sans remise (option replace). En voici quelques exemples :

sample(1:100, 1)             # choisir un nombre entre 1 et 100
sample(1:6, 10, replace = T) # lancer un dé 10 fois
sample(1:6, 10, T, c(.6,.2,.1,.05,.03,.02))   #  un dé non équilibré
urn <- c(rep("red",8),rep("blue",4),rep("yellow",3))
sample(urn, 6, replace = F)  # tirer 6 boules dans cette urne

Notons enfin que bien d'autres lois de probabilités moins usuelles sont disponibles dans des librairies séparées (evd, gld, stable, normalp,...). Notions de statistique inférentielleUn des buts de la statistique est d'estimer les caractéristiques d'une loi de probabilité à partir d'un nombre fini d'observations indépendantes de cette dernière. Par exemple, on pourrait s'imaginer observer un échantillon empirique issu d'une loi normale de moyenne et de variance inconnue avec pour but l'identification de ces paramètres inconnus. Ainsi par exemple la loi des grands nombres justifierait l'estimation d'une espérance mathématique par la moyenne empirique, et on comprend qu'intuitivement que plus la taille de l'échantillon est importante, meilleure sera l'estimation. La théorie de la statistique inférentielle permet en particulier d'évaluer de manière probabiliste la qualité de ce type d'identifications. Cette section en donne quelques illustrations sommaires avec l'aide de R.

Estimation ponctuelle

Nous savons que le ou les paramètres d'une loi de probabilité résument de manière théorique certains aspects de cette dernière. Les paramètres les plus habituels sont l'espérance mathématique, notée $\mu$ , la variance $\sigma^2$ , une proportion $\pi$ , une médiane , des quantiles, etc. Ce ou ces paramètres, génériquement notés $\theta$ sont en général inconnus et devront en général être approchés de manière optimale par des statistiques $\hat{\theta}$ calculées sur des échantillons aléatoires issus de la loi (ou population) étudiée. En pratique, la statistique calculée dépend de l'échantillon tiré et produira une estimation variable du paramètre inconnu. Ainsi par exemple si le paramètre inconnu est l'espérance $\mu$ , la moyenne empirique d'un échantillon $X_1, \dots, X_n$ issu de la loi est la variable aléatoire moyenne empirique $\hat{\mu}=\bar{X}_n = \sum_{i=1}^n X_i / n$ elle même distribuée selon une certaine loi de probabilité. Il est important de se souvenir que l'on ne réalise un échantillon qu'une seule fois et donc que l'on ne dispose que d'une seule valeur de l'estimateur $\hat{\theta}$ (estimation ponctuelle).

La loi forte des grands nombres permet d'affirmer que pour une loi admettant une espérance $\mu$ et une variance $\sigma^2$ , la moyenne empirique $\bar{X}_n$ converge vers $\mu$ alors que le théorème de la limite centrale dit que la loi de la moyenne empirique $\bar{X}_n$ peut être approchée de mieux en mieux quand la taille de l'échantillon tend vers l'infini par une loi normale d'espérance $\mu$ et de variance $\sigma^2/n$ . On peut illustrer ces propriétés par des expériences aléatoires appropriés, programmées avec R de la manière suivante.

Pour un échantillon de la loi uniforme sur de taille , calculons les moyennes empiriques successives et traçons la moyenne empirique en fonction de la taille de l'échantillon. On observe que la moyenne empirique converge bien vers la valeur $\mu=0.5$ représentée par une droite horizontale rouge sur le graphique 17.

n<-1000
X<-runif(n)
Y<-cumsum(X)
N<-seq(1,n, by=1)
plot(N, Y/N)
abline(h=0.5,col="red")

**Figure 17:** Illustration de la loi des grands nombres
$\includegraphics[width=6cm]{lng}$

Si l'on simule maintenant réalisations d'échantillons de tailles respectives et , issus d'une loi uniforme sur on peut tracer sur un même graphique l'histogramme des moyennes empiriques associées et illustrer le fait que cet histogramme est proche de la densité de la loi normale de moyenne $\mu=0,5$ et de variance $\sigma^2/n$ avec $\sigma^2=1/12$ .

X<-matrix(runif(500*10), ncol=10, nrow=500)
X1<-apply(X,1,mean) # 500 tirages de moyenne empirique 
Y<-matrix(runif(500*100), ncol=100, nrow=500)
Y1<-apply(Y,1,mean) # 500 tirages de moyenne empirique 
par(mfrow=c(1,2))
hist(X1,main="Taille d'échantillon 10",prob=T)
curve(dnorm(x,0.5,sqrt(1/120)),add=T)
hist(Y1,main="Taille d'échantillon 100",prob=T)
curve(dnorm(x,0.5,sqrt(1/1200)),add=T)

**Figure 18:** Illustration de la convergence en loi
$\includegraphics[width=6cm]{clt}$

Intervalles de confiance et test d'hypothèses

Un domaine très important de la statistique inférentielle est la construction d'intervalles de confiance (estimation ensembliste) et la construction de tests d'hypothèses sur les paramètres des lois qui régissent les observations faites. Le logiciel R couvre l'essentiel des besoins en probabilités et statistiques élémentaires avec en particulier ceux utiles pour l'estimation par intervalles de confiance et des tests de base, ainsi que plusieurs outils d'ajustements graphiques de distributions. Nous allons en donner un aperçu dans les sous-paragraphes suivants.

Estimation ensembliste et tests d'une proportion

L'illustration la plus fréquente de la notion d'estimation ensembliste est l'estimation par intervalle de confiance d'une proportion inconnue $\pi$ au vu d'une réalisation d'un échantillon de loi de Bernoulli. Par exemple, si lors d'un sondage d'une population vous observez la réponse de 100 personnes tirées au hasard dans la population et que vous observez que 42 parmi elles aiment la marque X, que pouvez vous dire de la probabilité $\pi$ qu'une personne tirée au hasard dans la population aime la marque X? Une première façon de répondre à cette question serait de proposer, comme dans les paragraphes précédents, une estimation ponctuelle de cette probabilité $\pi$ , donc pour cet exemple, $\hat{\pi}=0.42$ . Cette estimation dépend trop de la réponse du sondage et pour une autre réalisation peut être différente. Il serait donc opportun de proposer plutôt une fourchette de valeurs pour $\pi$ qui tienne compte de la variabilité de l'estimateur. Examinons cela de près : notons , ..., les variables de Bernoulli $B(1,\pi)$ indépendantes modélisant la réponse éventuelle de chaque individu parmi les tirés au hasard dans la population (dont l'effectif est très grand). Nous avons vu que l'estimateur ponctuel de $\pi$ est la moyenne empirique

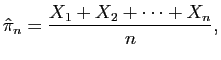
$\displaystyle \hat{\pi}_n= \frac{X_1+X_2+ \cdots + X_n}{n},$

et que, si

est grand, d'après le théorème de la limite centrale, on peut approcher la loi de la variable

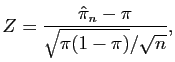
$\displaystyle Z = \frac{\hat{\pi}_n - \pi}{\sqrt{\pi(1-\pi)}/\sqrt{n}},$

par la loi $\mathcal {N}(0,1)$ d'une variable aléatoire normale centrée réduite. Si l'on est dans ces conditions on peut donc évaluer la distance de

à 0 avec une certaine probabilité. Par exemple, on peut affirmer, grâce aux propriétés de la loi normale, que $Z \in [-1,+1]$ avec une probabilité proche de 0.68, que $Z \in [-2,+2]$ avec une probabilité proche de 0.95, etc. En fait l'approximation normale de l'estimateur $\hat{\pi}_n$ , permet de construire un intervalle de confiance pour $\pi$ de niveau $(1-\alpha)$ avec $0<\alpha<1$ en résolvant l'inégalité

$\displaystyle \vert\pi-\hat{p}_n\vert \leqslant \Phi^{-1} (1-\alpha/2) \sqrt{\pi (1-\pi)}\sqrt{n}.$

(1)

Cela se fait par résolution d'une inéquation du second degré, mais à titre de simplification, après avoir ré-écrit l'équation (1) sous la forme d'un intervalle $\hat{\pi}_n \pm \Phi^{-1} (1-\alpha/2) \sqrt{\pi (1-\pi)}\sqrt{n}$ , nous allons approcher l'écart-type $\sqrt{\pi (1-\pi)}\sqrt{n}$ dans les bornes de cet intervalle par $\sqrt{\hat{\pi} (1-\hat{\pi})}\sqrt{n}$ , en justifiant cette approximation par la loi forte des grands nombres. Pour notre exemple numérique du début de ce paragraphe, on peut donc proposer pour la proportion inconnue $\pi$ d'individus préférant la marque X, la fourchette approchée

calculée avec

0.42 - qnorm(0.975)*sqrt(0.42*0.58)/sqrt{100}
0.42 + qnorm(0.975)*sqrt(0.42*0.58)/sqrt{100}

À titre d'exercice on pourra résoudre l'inégalité (1) et se passer ainsi de l'utilisation de la loi des grands nombres pour le calcul de l'intervalle de confiance.

Nous allons poursuivre cet exemple en illustrant par simulation le fait qu'un intervalle de confiance ne recouvre pas toujours la vraie valeur du paramètre $\pi$ . Ceci ce réalise de manière simple avec la fonction matplot et les commandes suivantes, qui produisent la figure 19 :

m <- 50; n<-20; Pi <- .5;  #  20  pièces à lancer   50 fois
p <- rbinom(m,n,Pi)/n # simuler et calculer l'estimation
ET<- sqrt(p*(1-p)/n) # estimer l'écart-type
alpha = 0.10 # seuil de signification
zstar <-qnorm(1-alpha/2)
matplot(rbind(p-zstar*ET, p+zstar*ET),rbind(1:m,1:m),type="l",lty=1)
abline(v=Pi) # trace la  verticale en Pi

**Figure 19:** Combien d'intervalles de confiance de niveau 80 % recouvrent-ils la vraie proportion $\pi =0.5$ ?
$% latex2html id marker 7645 \includegraphics[width=6cm]{ICprop}$

Bien évidemment la notion d'intervalle de confiance pour un paramètre est la notion duale d'un test bilatéral sur ce paramètre. Ainsi tester, au niveau de signification $\alpha$ , que la vraie proportion est $\pi_0$ contre son alternative $\pi\not= \pi_0$ au vu de la réalisation d'un échantillon, équivaut à regarder si l'intervalle de confiance pour $\pi$ an niveau $(1-\alpha)$ recouvre ou non $\pi_0$ . Ainsi pour notre exemple du sondage à propos de la marque X, ceci est réalisé avec la fonction prop.test.

prop.test(42,100,conf.level=0.95)

qui donne :

1-sample proportions test with continuity correction

data:  42 out of 100, null probability 0.5 
X-squared = 2.25, df = 1, p-value = 0.1336
alternative hypothesis: true p is not equal to 0.5 
95 percent confidence interval:
 0.3233236 0.5228954 
sample estimates:
   p 
0.42

On notera les bornes de l'intervalle corrigées, qui différent légèrement de celles que nous avions déterminé avec la loi des grands nombres. Le résultat affiché est une liste, dont on peut extraire les composants. Par exemple pour l'intervalle de confiance :

prop.test(42,100,conf.level=0.95)$conf.int

Les tests et l'estimation par intervalle issus d'autres lois suivent la même configuration.

Estimation ensembliste et tests sur la moyenne

Considérons à titre d'exemple l'estimation ensembliste de la moyenne $\mu$ au niveau de confiance $(1-\alpha)$ au vu d'une réalisation d'un échantillon gaussien , ..., d'espérance $\mu$ et de variance connue $\sigma^2$ . Nous savons que l'intervalle de confiance pour $\mu$ est de la forme $\bar{X}_n \pm \Phi^{-1}(1-\alpha/2) \sigma/\sqrt{n}$ . On peut construire une fonction simple pour son calcul comme suit :

ICsimple <-function(x,sigma,niv.conf=0.95){
n <- length(x)
xbar<-mean(x) 
alpha <- 1-niv.conf
zstar <- qnorm(1-alpha/2) 
ET <- sigma/sqrt(n)
xbar + c(-zstar*ET,zstar*ET)
}

qui donne, pour une réalisation x :

x<-c(175,176,173,175,174,173 ,173 ,176,173,179)
ICsimple(x,1.5)
[1] 173.7703 175.6297

De manière plus réaliste, la variance est plutôt inconnue et l'intervalle de confiance est calculé à l'aide de la loi de Student. En effet, si

est la racine carrée de l'estimation sans biais de la variance, on sait que la statistique $(\bar{X}_n - \mu)/ \sigma/\sqrt{n}$ suit la loi de Student à

degrés de liberté d'où l'intervalle de confiance $\bar{X}_n \pm qt(1-\alpha/2,n-1)* \sigma/\sqrt{n}$ . Ainsi par exemple pour la réalisation

de l'exemple précédent on trouve comme intervalle de confiance pour $\mu$ au niveau de confiance de 0.95, l'intervalle

, qui comme nous le constatons est plus long car la loi de Student a des ailes plus lourdes que celles d'une loi gaussienne. L'implémentation du test de Student est réalisée dans R avec la fonction t.test() qui non seulement calcule le test de l'hypothèse désirée sur $\mu$ mais retourne aussi l'intervalle de confiance. Cette même fonction permet de comparer les moyennes de deux échantillons gaussiens appariés ou non. Ainsi par exemple pour tester si

est un échantillon d'espérance $\mu=170$ , on utilisera t.test(x,alternative="two.sided", mu=170) qui donne :

	One Sample t-test

data:  x 
t = 7.6356, df = 9, p-value = 3.206e-05
alternative hypothesis: true mean is not equal to 170 
95 percent confidence interval:
 173.3076 176.0924 
sample estimates:
mean of x 
    174.7

et rejette l'hypothèse nulle puisque la p-valeur est $3.206 10^{-5}$ . Pour un test unilatéral, t.test(x,alternative="less", mu=170) donne :

	One Sample t-test

data:  x 
t = 7.6356, df = 9, p-value = 1
alternative hypothesis: true mean is less than 170 
95 percent confidence interval:
     -Inf 175.8284 
sample estimates:
mean of x 
    174.7

et accepte l'hypothèse $\mu \geqslant 170$ .

Test d'adéquation et d'indépendance

Pour terminer ce paragraphe, voici les tests du chi-deux d'ajustement et de contingence. Un test d'ajustement permet de décider si la distribution des valeurs d'une échantillon est correctement ajustée par une loi de probabilité spécifiée à l'avance. Par exemple, si on lance un dé 150 fois de manière indépendante et que l'on observe les fréquences suivantes

face	1	2	3	4	5	6
fréq.	22	21	22	27	22	36

on peut se demander si le dé est bien équilibré.

Pour cela il suffit d'évaluer la distance entre les fréquences observées et celles qui auraient dû être observées si le dé était bien équilibré. Cette distance est, dans le cas équilibré, distribuée selon une loi du chi deux à 5 degrés de liberté et est obtenue par :

freq <- c(22,21,22,27,22,36)
probs <- c(1,1,1,1,1,1)/6 
chisq.test(freq,p=probs)

qui donne :

     Chi-squared test for given probabilities
     data:  freq
     X-squared = 6.72, df = 5, p-value = 0.2423

confortant ainsi l'hypothèse d'un dé bien équilibré.

La même fonction peut être également utilisée pour tester l'indépendance des variables dans une table de contingence. On suppose observer deux variables catégorielles et , respectivement à et modalités. On observe ainsi indépendamment le couple sur une population de sujets. Soit alors $N_{ij}$ le nombre de sujets pour lesquels on a , de sorte que $\sum_{i=1}^I \sum_{j=1}^J N_{ij} = n$ . Les comptages observés peuvent être organisés en un tableau à double entrée :

			$\hdots$
	$n_{11}$	$n_{12}$	$\hdots$	$n_{1J}$
	$n_{21}$	$n_{22}$	$\hdots$	$n_{2J}$
$\vdots$	$\vdots$	$\vdots$	$\ddots$	$\vdots$
	$n_{I1}$	$n_{I2}$	$\hdots$	$n_{IJ}$

Le nombre total d'entrées de ce tableau de contingence est

. Les sommes marginales seront notées $n_{i+}$ , $n_{+j}$ et $n_{++}=n$ .

À titre d'exemple considérons, dans une étude d'accidents de voiture, les variables (port de ceinture, oui ou non ) et (gravité de la blessure, aucune, minimale, légère, grave) avec pour tableau observé :

		aucune	minimale	légère	grave
Ceinture	Oui	128213	647	359	42
	Non	65963	4000	2642	303

On peut alors se poser la question de savoir si le port de ceinture modifie la répartition des blessures, autrement dit, est-ce que les lignes de ce tableau sont indépendantes. Ceci est assez simple à réaliser dans R.

avecceinture<-c(12813,647,359,42)
sansceinture<- c(65963,4000,2642,303)
chisq.test(data.frame(avecceinture,sansceinture))

qui donne

	Pearson's Chi-squared test

data:  data.frame(avecceinture, sansceinture) 
X-squared = 59.224, df = 3, p-value = 8.61e-13

et montre l'influence évidente du port de la ceinture.

Régression linéaire simpleDans ce paragraphe nous allons examiner une modélisation particulière pour étudier (décrire, prédire, ...) une variable appelée variable expliquée (ou réponse ou variable dépendante) sur la base d'autres variables, appelées explicatives (ou covariables ou variables indépendantes). Nous nous resteindrons au cas d'une seule variable explicative d'où la notion de régression simple. Un modèle de régression linéaire simple décrit le cas particulier d'une seule variable explicative de type quantitatif (aléatoire ou déterministe) pour un phénomène physique régi par l'équation

$\displaystyle Y = aX+b+ \hbox{bruit al\'eatoire},$

(2)

le bruit étant une variable aléatoire centrée. À titre d'exemple, il est généralement admis que la fréquence théorique maximale du pouls

d'une personne est relié en moyenne à l'âge noté

par une équation du type

. Il y a deux manières d'interpréter le modèle (2) : soit on observe des réalisations indépendantes

, ...,

du couple de variables aléatoires

(comme pour l'exemple de l'étude de la fréquence théorique maximale du pouls), soit on observe des réalisations indépendantes de

en des valeurs de la variable explicative $x_1,\dots,x_n$ fixées à l'avance. Ceci ne modifie pas les calculs ni l'interprétation des résultats à condition de supposer que dans le cas où

est aléatoire, il est indépendant du bruit. Les coefficients

sont inconnus et on peut vouloir les identifier, par exemple pour prédire la réponse

en un point

quelconque. Dans la suite nous nous proposons d'illustrer les calculs et l'interprétation avec un exemple simulé, ainsi que sur des données expérimentales.

Considérons d'abord l'exemple d'une régression linéaire simple pour laquelle la droite de régression est donnée par l'équation . Cette droite est représentée par la droite de couleur bleue dans le graphique de gauche de la figure 20. Les observations se font en des points fixés, données par les abscisses , $i=1,\dots, 9$ des points rouges, d'ordonnées situés sur la droite. En chaque point on tire au hasard, 5 observations selon une loi gaussienne de moyenne et de variance , représentées par les points bleus sur le graphique du centre. En réalité, l'ensemble des données observées pour cet exemple simulé est le nuage des points du dernier graphique. La fonction permettant de tracer des densités gaussiennes à la verticale est :

sideways.dnorm<-function(wx,wy,values=seq(-4,4,.1),magnify=4,...){
# ... est constitué des moyennes et écart-types, 
# passés à la fonction dnorm 
# 
dens <- dnorm(x=values, ...)
x <- wx + dens * magnify
y <- wy + values
return(cbind(x,y))
}

et les graphiques de la figure 20 sont réalisés avec les commandes :

 
par(mfrow=c(1,3))
x<-seq(-8,8,2)
y <- 1 + .5*x 
fit <- lm(y~x)
plot(x,y, xlim=c(-10,10), ylim=c(-3, 7), pch=19,  
    cex=1.4,col="red",  main="équation de régression")
abline(fit, lwd=3, col="blue")
plot(x,y, xlim=c(-10,10), ylim=c(-8, 10), pch=19, cex=1.4
, main="Régression linéaire simple\navec erreurs gaussiennes"
, col="red")
abline(fit, lwd=3, col="blue")
where.normal.x<-sort(x)
xx<-NULL
zz<-NULL
# where.normal.x <- c(-4,0,4)
for(i in 1:length(where.normal.x)){
    where.x <- where.normal.x[i]
    where.y <- predict(fit, newdata=data.frame(x=where.x))
    xy <- sideways.dnorm(where.x=where.x, where.y=where.y, magnify=4)
    lines(xy)
    abline(h=where.y, lty=2,col="pink")
    abline(v=where.x, lty=2)
    xx<-c(xx,rep(where.x,5))
    z<-where.y+rnorm(5)
    zz<-c(zz,z)
    aux<-cbind(rep(where.x,5),z)
    points(aux,col="blue")
    }
plot(xx,zz,xlim=c(-10,10), ylim=c(-3, 7),main="les observations")

**Figure 20:** Simulation selon un modèle de régression simple avec bruit gaussien
$\includegraphics[width=15cm]{reglin1}$

Pour continuer avec ce modèle simulé de régression linéaire simple, on voudrait à partir des observations estimer les coefficients et de la droite modélisant les comme des réalisations de variables aléatoires , non corrélées, de moyennes et de variance constante $\sigma^2$ . Pour cela on utilise le principe des moindres carrés qui consiste à minimiser la fonction de perte :

$\displaystyle \ell_2(a,b) = \sum_{i=1}^n[ y_i - (ax_i+b) ]^2,$

et dont l'optimum est solution du système linéaire des équations normales :

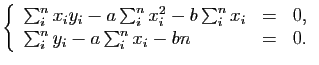$\displaystyle \left\{ \begin{array}{lcr} \sum_{i}^n x_iy_i - a\sum_{i}^nx_i^2... ...& = & 0,\ \sum_{i}^ny_i - a\sum_{i}^nx_i - bn & = & 0. \end{array} \right.$

En notant $\mathbf{y}$ le vecteur des observations, $\mathbf{x}$ le vecteur de composantes

et $\bar {\text{cov}}$ , $\bar v(\mathbf{x})$ , $\bar y$ et $\bar x$ les moments empiriques associés, on obtient les solutions :

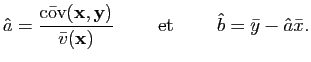
$\displaystyle \hat a= \frac{\bar{\text{cov}}(\mathbf{x},\mathbf{y})}{\bar v(\mathbf{x})} \qquad\mbox { et } \qquad\hat b = \bar y - \hat a \bar x.$

On remarquera ici que les estimateurs obtenus sont les versions empiriques des coefficients de régression $\beta_2=\frac{\hbox{cov}(Y,X)}{\hbox{var}(X)}$ et $\beta_1= E(Y) - \beta_2 E(X)$ .

La dernière équation montre que la droite des moindres carrés passe par le centre de gravité du nuage $\{(x_i,y_i),\quad i=1,\dots, n\}$ . On pouvait s'attendre à ce résultat car la meilleure prédiction de lorsque $x =\bar x$ doit bien être $\bar y$ .

Pour ce cas particulier l'estimation sans biais de la variance $\sigma^2$ est donnée par

$\displaystyle \hat{\sigma}^2 = \frac{1}{n-2}\sum_{i=1}^n[ y_i - (\hat{a}x_i+\hat{b}) ]^2.$

Pour l'exemple des données simulées, l'ajustement des moindres carrés s'obtient avec la commande lm() et on obtient la figure 21 avec les commandes

{plot(xx,zz,xlim=c(-10,10), ylim=c(-3, 7),
      main="Ajustement des moindres carrés")}
fitb<-lm(zz~xx)
abline(fitb,lty=2,col="blue",lwd=3)
abline(fit,lty=1,col="black")

**Figure 21:** Ajustement de la régression simple sur des données simulées. La droite en trait plein est le modèle exact, la droite en pointillés est estimée.
$\includegraphics[width=10cm]{reglin2}$

Les sorties R associées à un ajustement d'un jeu de données par un modèle de régression linéaire à l'aide de la fonction lm() peut s'obtenir par un summary() de l'objet ajusté.

fitb<-lm(zz~xx)
summary(fitb)

qui donne

Call:
lm(formula = zz ~ xx)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.94795 -0.62929 -0.08101  0.43664  2.36308 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.86451    0.14747   5.862 5.79e-07 ***
xx           0.50503    0.02856  17.685  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 0.9892 on 43 degrees of freedom
Multiple R-squared: 0.8791,	Adjusted R-squared: 0.8763 
F-statistic: 312.8 on 1 and 43 DF,  p-value: < 2.2e-16

On y retrouve une description par quantiles de la distribution des valeurs de la réponse (ici zz) puis les estimations ponctuelles de l'ordonnée à l'origine et de la pente, avec l'estimation de leurs écart-types et des p-valeurs des tests de nullité de chacun des paramètres (qui ne tiennent pas compte de leur corrélation). Enfin, l'estimation ponctuelle de l'écart-type est donnée sur la ligne suivant le tableau des coefficients. On y retrouve aussi les valeurs estimées du coefficient de détermination et la p-valeur du test d'absence d'influence du régresseur. Comme d'habitude, le résultat est une liste dont on peut extraire les composants. Par exemple pour l'ordonnée à l'origine, puis la pente :

fitb$coefficients[1]
fitb$coefficients[2]