À deux ou trois lieues près

Par Décret Royal du Conseil des Indes de la Couronne de Castille, VAN LANGREN a écrit un mémoire avec les règles théoriques et pratiques pour que les pilotes calculent les degrés de longitude à partir de la méthode du point fixe et par navigation à latitude constante. Et ayant corrigé la Géographie, ils pourront savoir combien de degrés il y a entre le navire et l'endroit où il désire aller, sans qu'il y ait nécessité de conjecture ni de quadrature, comme on le faisait jusqu'ici, à grand peine et perte de navires. Tout étant si exact que l'erreur sera moindre que deux ou trois lieues aux latitudes moyennes et de quatre ou cinq lieues à l'équateur.

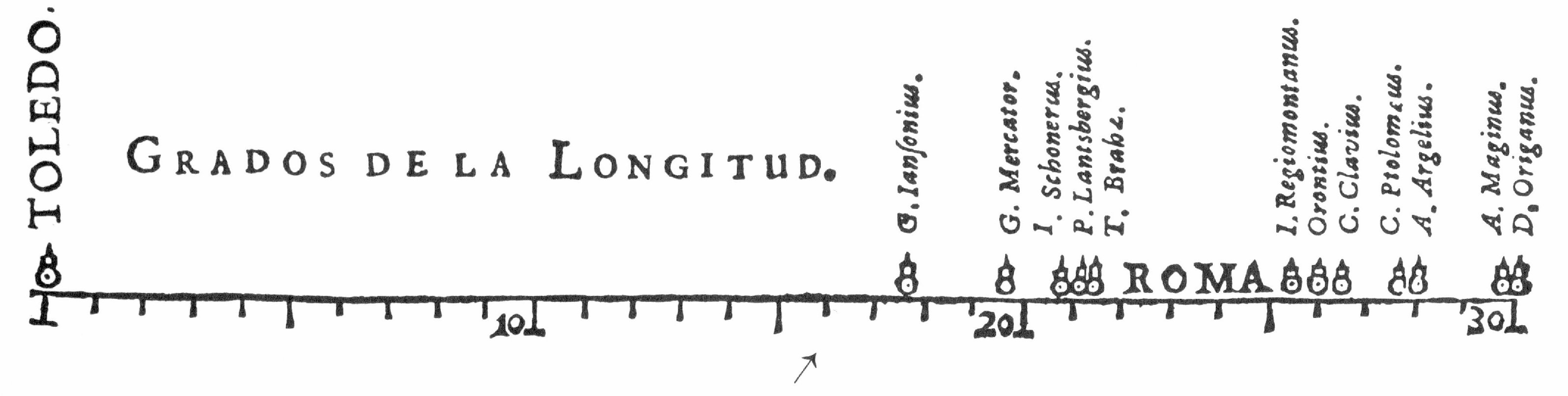
Le secret important de la longitude a été recherché par d'éminents scientifiques. Comme les rois catholiques ont offert beaucoup d'argent à celui qui le résoudrait, beaucoup ont tenté de le résoudre, d'où ont résulté beaucoup de dépenses et d'abus, d'où vient que les rois se défient des promesses de ceux qui disent détenir la solution.

En 1644, Michael Florent van Langren (1598-1675) signe sa lettre en tant que «cosmographe et mathématicien de Sa Majesté en Flandre»¹. Sa majesté Philippe IV d'Espagne, règne alors sur une bonne partie de l'Europe de l'Ouest et de l'Amérique du Sud. Faire en sorte que Ses navires, chargés de l'or du Pérou ou des marchandises européennes parviennent à bon port, c'est s'assurer Sa reconnaissance, sonnante et trébuchante. Or si l'on sait depuis longtemps déterminer la latitude d'un lieu par observation des étoiles visibles, le calcul de la longitude, sans horloge d'une précision suffisante, est d'une toute autre difficulté. L'enjeu pour van Langren est de convaincre Sa Majesté qu'il peut faire mieux que les données disponibles du temps. «Deux ou trois lieues», soit une dizaine de kilomètres, cela peut vous paraître beaucoup quand il s'agit de ne pas manquer l'entrée d'un port. Mais van Langren sait que c'est bien plus précis que les données disponibles en son temps. Pour mieux en souligner la grande variabilité, il a une idée : il représente les estimations connues de la différence de longitude entre Tolède et Rome sur un axe horizontal (figure 22).

Figure 22: M. F. van Langren : représentation graphique des différences de latitude estimées entre Tolède et Rome. La flèche indique la valeur exacte.

C'est la toute première représentation graphique de données statistiques. Van Langren faisait tout son possible pour emporter l'adhésion de Sa Majesté (et la gratification qui s'ensuivrait) ; et, si on peut oser cet anachronisme, il n'y avait pas photo ! Les cartes disponibles surestimaient toutes la longitude exacte de plusieurs degrés, jusqu'à plus de 10. Or à la latitude de Rome, 10 degrés de longitude, cela fait tout de même la bagatelle de 1000 kilomètres. Autant vous dire que les pilotes de Sa Majesté avaient plus intérêt à compter sur leur expérience de la navigation que sur leurs cartes !