Les tâtonnements de Leibniz

S'il y a bien un fil directeur dans l'uvre foisonnante de Leibniz (1646-1716), c'est son souci constant d'améliorer l'«art d'inventer». Pour lui, il convient avant tout de désencombrer l'esprit du savant de tout ce qui peut être automatisé. D'où en particulier les recherches que Leibniz mènera toute sa vie sur les calculateurs mécaniques. En outre, Leibniz était parfaitement conscient de l'importance d'un choix judicieux de notations, permettant d'automatiser les calculs avec des symboles. Il appelle cela l'«art caractéristique», (du choix des caractères), lui-même soumis à l'art combinatoire (de combiner ces caractères)¹. Ce thème était déjà présent dès sa thèse, écrite en 1666 à l'âge de 20 ans : il y inventait un «alphabet de la pensée humaine». Ce souci d'automatiser les procédures par un choix de notations judicieux l'a conduit pour le calcul différentiel, à définir celles que vous utilisez encore. Le même souci préside encore à ses travaux sur la résolution de systèmes linéaires, et la détermination de solutions communes aux équations algébriques. C'est ainsi qu'il est amené au fil des années à développer les déterminants. Il n'est pas l'auteur de la théorie complète, mais plutôt d'un ensemble de règles empiriques non démontrées, qui préfigurent néanmoins les propriétés que vous avez apprises dans ce chapitre. D'ailleurs il n'existe pas de traité publié par Leibniz sur les déterminants. Seulement un corpus de manuscrits et de lettres en latin, adressées à quelques uns de ses 1100 correspondants recensés. Pourquoi un tel intérêt pour les systèmes linéaires ? Leibniz pensait que n'importe quelle résolution d'équation (algébrique, différentielle ou autre) pouvait se ramener à la résolution d'un système linéaire. Au vu des méthodes numériques développées depuis deux siècles, c'était singulièrement prémonitoire !

Dans le cadre de son «art caractéristique», Leibniz inventa plus cinquante manières d'utiliser des nombres fictifs ; deux seulement furent publiées. Voici une de ses façons d'écrire une équation linéaire quelconque :

$$10+11x+12y=0\;.$$

Comprenez : 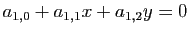$a_{1,0}+a_{1,1}x+a_{1,2}y=0$, ou bien 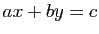$ax+by=c$ : que préférez-vous ? Paradoxalement, ces multiples choix de notations pour les systèmes linéaires, le fait de ne pas distinguer premier et second membre, semblent l'avoir handicapé plutôt qu'aidé dans ses lents tâtonnements vers la définition du déterminant. Ayant perçu assez tôt que les quantités qui apparaissaient dans les solutions de systèmes linéaires étaient des sommes de produits de coefficients, il a mis très longtemps à dégager la règle de l'alternance de signe. Il entrevoit cette règle dès 1678.

Ainsi nous avons une règle de laquelle la valeur d'une inconnue linéaire peut être écrite sans aucun calcul.

C'était trop optimiste. Son heuristique ne se généralise pas encore. Prudent, il écrit :

Ce théorème méritait d'être démontré exactement, ce qui se ferait par cette subtile analyse-là qui prescrit les lois au calcul même sans calcul.

Voici la règle des signes en 1683.

Soit un terme quelconque positif ou négatif : les termes qui se distinguent de ce terme par un nombre pair de coefficients sont affectés du signe opposé. Ceux qui se distinguent par un nombre impair de coefficients sont affectés du même signe.

Encore une autre, la même année :

Les membres qui n'ont qu'un seul coefficient commun ou un nombre impair de tels coefficients ont des signes opposés. Ceux qui ont deux ou un nombre pair de coefficients communs ont le même signe.

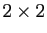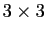Ce n'est toujours pas ça : Leibniz essaie de deviner le résultat en décortiquant les systèmes $2\times 2$ et $3\times 3$ qu'il résoud, mais la généralisation n'est pas évidente. Petit à petit, il parvient à dégager la notion de permutation des indices.

Les permutations des indices droits ont le même signe si elles résultent l'une de l'autre par un changement cyclique. Les autres permutations ont un signe opposé.

Enfin en 1684, il tient son succès.

Dans cette tentative, j'ai résolu le problème tandis qu'auparavant j'avais toujours essuyé un échec. Voici un exemple insigne de l'art combinatoire.

La règle qu'il énonce alors est bien la bonne :

Deux termes qui se distinguent l'un de l'autre seulement par un nombre impair de transpositions des indices gauches ou droits ont des signes opposés. Ceux qui se distinguent l'un de l'autre par un nombre pair ont le même signe.

S'il a fallu autant de temps à Leibniz pour comprendre comment développer un déterminant, peut-être n'est-ce pas si évident ?