Bases de numération

Le but de cette section est de définir un système d'écriture qui permette de manipuler aisément les nombres entiers, en particulier d'expliciter facilement les opérations addition et multiplication.

Pour simplifier les notations, la multiplication sur $\mathbb{N}$ sera notée pour $a\times b$ , le résultat de la multiplication de par itérée fois sera noté et l'inégalité stricte pour $a\leqslant b$ et $a\neq b$ .

On décide de représenter les premiers entiers par un symbole unique appelé chiffre et on cherche un moyen d'utiliser ces symboles pour écrire tous les nombres entiers. Deux symboles ont déjà été définis : 0 pour le plus petit élément de $\mathbb{N}$ et pour . Traditionnellement on note pour , pour , pour , pour , pour , pour , pour , pour , pour , pour , pour , pour , pour , pour ...

Etant donné un nombre entier appelé base, par exemple , , , ou , on peut proposer l'algorithme suivant pour dénombrer un ensemble :

on fait autant de paquets de éléments qu'il est possible, puis autant de paquets de paquets et ainsi de suite...

Remarquons qu'à la -ième étape, on obtient des regroupements de éléments.

Par exemple pour , considérons l'ensemble $E=\{\clubsuit\clubsuit\clubsuit\clubsuit\clubsuit\clubsuit\clubsuit\}$ et appliquons l'algorithme

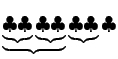
$\displaystyle \underbrace{\underbrace{\clubsuit\clubsuit} \underbrace{\clubsuit\clubsuit}}\underbrace{\clubsuit\clubsuit}\clubsuit$

nous obtenons un paquet de

paquets, qui regroupe donc

éléments, plus un paquet de

éléments, plus

élément. Le nombre d'éléments de

pourrait alors être représenté par le triple symbole $\overline{111}$ , le premier 1 à gauche correspondant au nombre de paquets de paquets, le second

au nombre de paquets restant et le dernier

au nombre d'éléments distincts.

L'algorithme se formalise de la manière suivante : écrire un nombre entier sous la forme

$\displaystyle x=x_n a^n+\dots+x_1 a+x_0, 0\leqslant x_i<a,$

appelé développement de

dans la base

. Si cette écriture est unique le nombre

pourrait alors être représenté par le multi-symbole $\overline{x_n\dots x_1x_0}$ .

Proposition 10 Si $a\in\mathbb{N}$ vérifie , la suite de terme général est strictement croissante et non majorée.

Démonstration : Puisque

, la compatibilité de la relation d'ordre avec la multiplication implique $a^n<a^{n+1}$ car

est non nul. La suite $(u_n)_{n\in\mathbb{N}}$ est donc croissante.

Nous devons prouver que pour tout $b\in\mathbb{N}$ , il existe $n\in\mathbb{N}$ tel que . Puisque $\mathbb{N}$ est archimédien (cf. Proposition 9), il suffit de montrer que $na\leqslant a^n$ pour tout tel que $1\leqslant n$ .

Pour on a bien . Supposons que $na\leqslant a^n$ . Puisque $1\leqslant n$ et , soit $2\leqslant a$ , on a

$\displaystyle (n+1)a\leqslant 2(na)\leqslant 2a^n\leqslant aa^n\leqslant a^{n+1}.$

On a donc montré par récurrence que $na\leqslant a^n$ pour tout

tel que $1\leqslant n$ . $\square$

Théorème 2 Pour tout $a\in\mathbb{N}$ et tout $b\in\mathbb{N}^*$ , il existe des entiers et uniques tels que

$\displaystyle a=bq+r$ et $\displaystyle \quad 0\leqslant r<b.$

Démonstration : On considère l'ensemble $A=b\mathbb{N}\cap\{x\in\mathbb{N} \vert x\leqslant a\}$ , où $b\mathbb{N}=\{x\in\mathbb{N} \vert \exists n\in\mathbb{N}, x=bn\}$ . L'ensemble

contient 0 et est majoré par

, il possède donc un plus grand élément

. L'élément

ainsi défini est unique et vérifie $bq\leqslant a<b(q+1)$ . On note

la solution de l'équation

, qui existe puisque $bq\leqslant a$ , elle vérifie $0\leqslant r<b$ puisque

. $\square$

L'opération définie dans le théorème s'appelle la division euclidienne de par , est le quotient de la division et le reste. Si , on dit que est divisible par .

Théorème 3 Si $a\in\mathbb{N}$ vérifie , tout nombre entier s'écrit de manière unique

$\displaystyle x=x_n a^n+\dots+x_1 a+x_0, 0\leqslant x_i<a, 1 \leqslant i\leqslant n,$ et $\displaystyle x_n\neq 0\;.$

Démonstration :

Unicité : Supposons qu'un tel développement existe alors

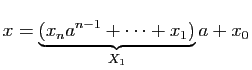$\displaystyle x=\underbrace{(x_na^{n-1}+\dots+x_1)}_{X_1}a+x_0$ et $\displaystyle \quad x_0<a.$
Les nombres et sont respectivement le reste et le quotient de la division euclidienne de par , ils sont donc déterminés de manière unique. Si on pose

$\displaystyle X_k=x_na^{n-k}+\dots+x_{k+1}a+x_k$
on remarque que est le reste de la division euclidienne de par et $X_{k+1}$ son quotient. En posant une récurrence immédiate prouve que les sont déterminés de manière unique.
Existence : Pour fixé dans $\mathbb{N}$ , les conditions

$\displaystyle y_0=x,\quad y_k=ay_{k+1}+x_k$ avec $\displaystyle \quad x_k<a$
déterminent par récurrence deux suites $(x_k)_{k\in\mathbb{N}}$ et $(y_k)_{k\in\mathbb{N}}$ . Nous allons prouver que la suite $(y_k)_{k\in\mathbb{N}}$ est stationnaire identiquement égale à 0 à partir d'un certain rang. Remarquons que, puisque , la suite $(y_k)_{k\in\mathbb{N}}$ vérifie

$\displaystyle 2y_{k+1}\leqslant ay_{k+1}\leqslant y_k,$
ce qui implique que $2^ky_k\leqslant x.$ Nous avons vu dans la preuve de la Proposition 9 que $2k\leqslant 2^k$ , on en déduit donc que $2ky_k\leqslant x$ et par conséquent dès que en raison de la compatibilité de la relation d'ordre avec la multiplication.
On désigne par le plus grand entier tel que $y_k\neq 0$ . Par définition de et de la suite $(y_k)_{k\in\mathbb{N}}$ , on a

$\displaystyle y_n=x_n$ et $\displaystyle \quad y_{n-k}=x_na^k+\dots +x_{n-k}, k=1,\dots ,n,$
en particulier pour , on obtient

$\displaystyle x=y_0=x_n a^n+\dots+x_1 a+x_0.$

$\square$

Notons que dans la base , le nombre entier s'écrit toujours $\overline{10}$ puisque $a=(1\times a)+0$ .

La base communément utilisée est , que l'on appelle la base dix, et tout nombre entier s'écrit alors en utilisant les chiffres et . L'usage courant veut que l'on écrive simplement pour $\overline{545}$ lorsqu'il n'y a pas d'ambiguïté sur la base choisie.

En informatique les bases et sont souvent utilisées, c'est ce qui est appelé système de numération binaire et système de numération hexadécimale.

Exemple : Si s'écrit $\overline{125}$ en base dix, il s'écrit $\overline{1111101}$ en binaire et $\overline{7D}$ en hexadécimal.

La démonstration de l'existence du développement dans une base fixée donne un algorithme pour calculer les chiffres qui apparaissent dans l'écriture d'un nombre entier dans cette base. Le premier chiffre de droite est donné par le reste de la division euclidienne de par , le second chiffre par le reste de la division euclidienne du quotient de la division précédente par et ainsi de suite jusqu'à l'obtention d'un quotient nul.

Relation d'ordre et numération

On considère le problème suivant : étant donnés deux entiers et , peut-on déterminer facilement si $x\leqslant y$ à partir de leur écriture dans une base donnée.

Fixons une base arbitraire. L'unicité du développement d'un entier relativement à la base implique que si et seulement si ils ont même écriture dans la base .

Lemme 1 Si $x\in\mathbb{N}$ s'écrit $\overline{x_n\dots x_0}$ dans la base , alors $a^n\leqslant x< a^{n+1}$ .

Démonstration : L'hypothèse du lemme se traduit par

$\displaystyle x=x_n a^n+\dots+x_1 a+x_0.$

Par conséquent $a^n\leqslant x_na^n\leqslant x$ puisque $1\leqslant x_n$ . Montrons par récurrence sur

que $x< a^{n+1}$ . Si

. Supposons l'inégalité vraie pour les nombres dont l'écriture dans la base

contient

chiffres. Soit

qui s'écrit $\overline{x_{n+1}x_n\dots x_0}$ , alors

$\displaystyle x=x_{n+1}a^{n+1}+y,$

avec

qui s'écrit $\overline{x_n\dots x_0}$ dans la base

et par conséquent on obtient

$\displaystyle x< x_{n+1}a^{n+1}+a^{n+1}\leqslant a^{n+1}(x_{n+1}+1)\leqslant a^{n+2}$

en utilisant l'hypothèse de récurrence et le fait que $x_{n+1}<a$ . $\square$

Supposons que et s'écrivent respectivement $\overline{x_n\dots x_0}$ et $\overline{y_m\dots y_0}$ dans la base et que $x\neq y$ .

Supposons que alors $n+1\leqslant m$ et puisque , le Lemme 1 implique

$\displaystyle x< a^{n+1}\leqslant a^m\leqslant y,$

d'où

Nous avons donc prouvé que :

Si deux entiers s'écrivent dans une même base avec un nombre de chiffres différent, le plus petit est celui dont l'écriture possède le moins de chiffres.

Supposons que . Puisque $x\neq y$ , il existe $1\leqslant r\leqslant n+1$ tel que pour tout $r\leqslant i$ et $x_{r-1}<y_{r-1}$ . On déduit alors du Lemme 1 que

$\displaystyle x$	$\displaystyle =x_n a^n+\dots+x_{r-1}a^{r-1}+x_{r-2}a^{r-2}+\dots+x_1 a+x_0$
	$\displaystyle < x_n a^n+\dots+x_{r-1}a^{r-1}+a^{r-1}$
	$\displaystyle < x_n a^n+\dots+(x_{r-1}+1)a^{r-1}$
	$\displaystyle < x_n a^n+\dots+y_{r-1}a^{r-1}$
	$\displaystyle < y$

Nous avons donc prouvé que :

Si deux entiers s'écrivent dans une même base avec un même nombre de chiffres et si en partant de la gauche les chiffres sont tous égaux jusqu'au rang , alors le plus petit des deux est celui qui a le plus petit chiffre de rang .

Lois de composition internes et numération

Soient et deux nombres entiers qui s'écrivent respectivement $\overline{x_n\dots x_0}$ et $\overline{y_m\dots y_0}$ dans la base , on cherche un mécanisme pour déterminer l'écriture dans la base des nombres et $x\times y$ .

Comme et $\times$ sont toutes deux commutatives, on peut supposer sans perte de généralité que $m\leqslant n$ .

$\bullet$ Cas de l'addition

Si $m\neq n$ on pose $y_n=\dots=y_{m+1}=0$ . Les propriétés de commutativité et d'associativité de et de distributivité de $\times$ par rapport à donnent

$\displaystyle x+y=(x_n+y_n) a^n+\dots+(x_1+y_1) a+(x_0+y_0).$

Si pour tout $i=0,\dots,n$ ,

, le développement ci-dessus correspond au développement de

dans la base

Sinon supposons que l'un des entiers est supérieur ou égal à , alors

$\displaystyle x_i+y_i=a+z_i\quad {\rm avec}\quad z_i<a$

et le nombre

s'écrit alors $\overline{1z_i}$ dans la base

. Par suite $(x_i+y_i)a^i=a^{i+1}+z_ia^i$ et $x_{i+1}+y_{i+1}$ doit être remplacé par $x_{i+1}+y_{i+1}+1$ , c'est le mécanisme de la retenue.

En conclusion, l'écriture dans la base du résultat de l'addition de deux entiers nécessite seulement la connaissance de la table d'addition en base des nombres dont l'écriture en base ne possède qu'un seul chiffre.

$\bullet$ Cas de la multiplication

Grâce à la distributivité de $\times$ par rapport à et à l'associativité de $\times$ , on a

$\displaystyle xy=x_n(a^ny)+\dots+x_1(ay)+x_0y.$

On est donc ramené

1) à multiplier un entier par une puissance de la base,

2) à multiplier un entier par un nombre strictement inférieur à la base et qui s'écrit donc avec un seul chiffre,

3) à faire des additions.

- Multiplication par

Cherchons l'écriture en base de . On a

$\displaystyle a^ky=ya^k=y_ma^{m+k}+\dots+y_0a^k$

s'écrit donc

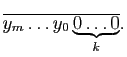
$\displaystyle \overline{y_m\dots y_0\underbrace{0\dots 0}_{k}}.$

L'existence des

chiffres 0 dans la partie droite de l'écriture de

en base

, explique le décalage dans la disposition pratique de la multiplication.

Exemple : En base avec , effectuons la multiplication de $\overline{45}$ par $\overline{101}$ , on aura

$\displaystyle \overline{45}\times \overline{101}=(4a+5)(a^2+1)=(4a^3+5a^2)+(4a+5)=\overline{4500}+\overline{45}$

qui en pratique s'écrit

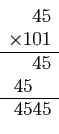
$\begin{displaymath} \begin{array}{r} 45\\ \times 101 \hline 45\\ 45 \hline 4545 \end{array}\end{displaymath}$

- Multiplication par un entier strictement inférieur à

Soit , alors $by=by_ma^m+\dots+by_0$ . Si pour tout $i=0,\dots,m$ , c'est fini sous réserve de connaître la table de multiplication en base des nombres dont l'écriture en base ne possède qu'un seul chiffre.