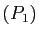
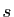 est injective,
est injective,
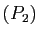
-
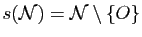 ,
,
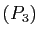
- Si
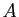 est une partie de
est une partie de
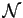 telle que si
telle que si 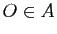 et
et
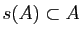 alors
alors
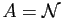 .
.
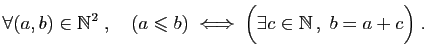
- réflexive car pour tout
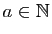 ,
, 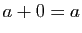 ,
donc
,
donc
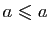 .
.
- antisymétrique car si
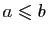 et
et
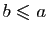 ,
alors il existe
,
alors il existe
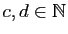 tels que
tels que 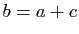 et
et
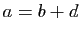 . Par conséquent
. Par conséquent 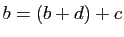 et puisque
et puisque 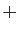 est associative
et que tout élément est régulier pour
est associative
et que tout élément est régulier pour 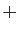 , on en déduit
, on en déduit 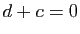 ,
ce qui entraîne
,
ce qui entraîne 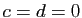 (propriété de l'addition),
soit
(propriété de l'addition),
soit 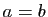 .
.
- transitive car si
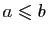 et
et
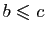 ,
alors il existe
,
alors il existe
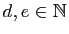 tels que
tels que 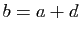 et
et
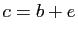 . Par conséquent
. Par conséquent
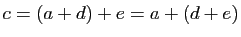 car
car 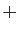 est associative, donc
est associative, donc
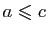 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales